��Ŀ����
����Ŀ����һ����Ϊl=1m��ľ��A�������㹻����ˮƽ�����ϣ�ȡһ�dz�����ľ��B��A��ס��B�������ڱڼ�ľ���ΪL=9m��A��B������ͬ����Ϊm=1kg��������Ķ�Ħ�������ֱ�Ϊ��A=0.2�ͦ�B=0.3����ʼʱA��B�����ڱڽӴ�����������ͬ�ij��ٶ�v0=28m/s�����˶�����֪A��B�������ڱڷ�������ײʱ�伫�̣��ɺ��Բ��ƣ�������ײ��A��B���ཻ���ٶȣ�A��B�����������Ӵ����������ٶ�g=10m/s2 �� ��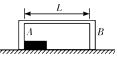
��1����ʼ�˶����ʱ��A��B������һ����ײ��
��2������v0δ֪�������������ֲ��䣬��
��ҪʹA��B���ͬʱֹͣ������A��B����Ӵ������ٶ�v0Ӧ�����������
��ҪʹB��ͣ�£������ȫ��ͣ��ʱA�˶���B�ұڸպ�ֹͣ�����ٶ�v0Ӧ�����������
���𰸡�
��1���⣺ľ���ľ�зֱ����ȼ����˶������ٶȴ�С�ֱ�Ϊ��
aA=��Ag=2 m/s2��
aB=��Bg=3 m/s2
�辭��ʱ��T������һ����ײ�����У�
L��l=xA��xB= ![]()
�������ݵã�T=4 s
�𣺿�ʼ�˶���4s��ʱ��A��B������һ����ײ
��2���⣺����һ���ɣ�1���ɼ�ľ�顢ľ�о���ʱ��t1=2T����������Ӵ�ʱ�ٶ�ǡ����ͬ��ͬ���ɵã�ľ�顢ľ�о���ͬ��ʱ��t2=2T��ÿ������ʱ�ٶȾ���С��v=20 m/s��
��ҪʹA��B���ͬʱֹͣ������A��B����Ӵ���v0=20n��m/s�� ��n=1��2��3������
��ҪʹB��ͣ�£����ٶȱ�������v0=n��v+v ��n=1��2��3������0��v����BgT=12 m/s��
����k����ײ��A�˶���B����ڣ����й�ͬ�ٶ�v������ABһ������˶���ֱ��ֹͣ��Aǡ���˶���B���ұ�ֹͣ��L��l=xA��xB= ![]() ��
�� ![]() �����v=4
�����v=4 ![]() m/s
m/s
����ҪʹB��ͣ�£������ȫ��ͣ��ʱA�˶���B���ұڸպ�ֹͣ�����ٶ�v0=��20n+4 ![]() ��m/s��n=1��2��3������
��m/s��n=1��2��3������
��������A��B��v��tͼ����ͼ��ʾ��
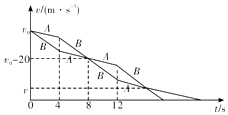
��ҪʹA��B���ͬʱֹͣ������A��B����Ӵ���
v0=n��v=20n��m/s����n=1��2��3������
��ҪʹB��ͣ�£������ȫ��ͣ��ʱA�˶���B���ұڸպ�ֹͣ��
v0=n��v+v
�� ![]() ��
�� ![]() =L��l
=L��l
v=4 ![]() m/s
m/s
��v0=��20n+4 ![]() ��m/s��n=1��2��3����
��m/s��n=1��2��3����
������v0δ֪�������������ֲ��䣬��
��ҪʹA��B���ͬʱֹͣ������A��B����Ӵ������ٶ�v0Ӧ����v0=20n��m/s����n=1��2��3������
��ҪʹB��ͣ�£������ȫ��ͣ��ʱA�˶���B�ұڸպ�ֹͣ�����ٶ�v0Ӧ����v0=��20n+4 ![]() ��m/s��n=1��2��3����
��m/s��n=1��2��3����
����������1���ȸ���ţ�ٵڶ�������ü��ٶȣ������ȱ���ֱ���˶�����������һ����ײ��ʱ�䣻
��2��ľ���ľ���������̶����غ�ͻ�е���غ㣬�г���ʽ��⣮����ľ�顢ľ�е��˶��������˶�ѧ��ʽ�ͼ��ι�ϵ��⣮
�����㾫����ͨ����������ȱ���ֱ���˶����ٶȡ�λ�ơ�ʱ��Ĺ�ϵ�������ٶȹ�ʽ��V=V0+at��λ�ƹ�ʽ��s=v0t+1/2at2���ٶ�λ�ƹ�ʽ��vt2-v02=2as�����ϸ�ʽ��Ϊʸ��ʽ��Ӧ��ʱӦ�涨������Ȼ���ʸ����Ϊ��������⣬ͨ��ѡ���ٶȷ���Ϊ�������Ǹ�������һ�µ�ȡ��+��ֵ�����������෴��ȡ��-��ֵ�����Խ����⣮

 �����Ծ�ϵ�д�
�����Ծ�ϵ�д� �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д�