题目内容
16.为研究人们用绳索跨山谷过程中绳索拉力的变化规律,同学们设计了如图(a)所示的实验装置,它们将不可伸长轻绳的两端通过测力计(不及质量及长度)固定在相距为D的两立柱上,固定点分别为M和N,M低于N,绳长为L(L>D).他们首先在绳上距离M点10cm处(标记为C)系上质量为m的重物(不滑动),由测力计读出绳MC、NC的拉力大小TM和TN,随后改变重物悬挂点的位置,每次将M到C点的距离增加10cm,并读出测力计的示数,最后得到TM、TN与绳MC长度之间的关系曲线如图(b)所示,由实验可知: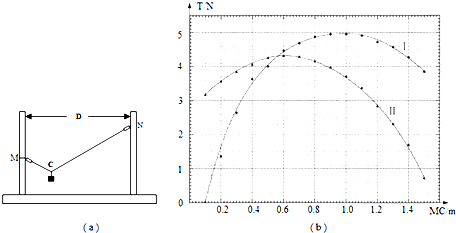
(1)曲线Ⅰ中拉力最大时,C与M点的距离为100cm,该曲线为TN(选填:TM或TN)的曲线.
(2)若用一个光滑的挂钩将该重物挂于绳子上,待稳定后,左端测力计上的示数为4.3N,MC与水平方向的夹角为0.37(用正弦值表示)(第2问结果均保留两位有效数字).
分析 (1)选取结点C为研究的对象,对它进行受力分析,根据结点C的受力分析,利用图象给出的信息即可分析判断.
(2)由图可知当物体通过滑轮挂在绳上时两绳子的拉力及物体的重力大小,根据几何关系可求得夹角大小.
解答 解:选取结点C为研究的对象,受力如图,
水平方向:TMsinα=TNsinβ
竖直方向:TMcosα+TNcosβ=G
由图可得,当α=β时,两个绳子上的拉力相等,该处离M比较近.
又C到M与N的距离相等时,受力如图:
水平方向仍然满足:TMsinα=TNsinβ
由于α>β
所以:TM<TN
所以曲线Ⅱ是TM的曲线,曲线Ⅰ是TN的曲线.
由图,曲线Ⅰ中拉力为最大时,C与M点的距离为100cm.
若用一个光滑的挂钩将该重物挂于绳子上,待稳定后,绳子两次的拉力相等,对应图象的交点,为4.3N;
由题目的图可得,在曲线Ⅰ、Ⅱ相交处,可读出绳的拉力T0=4.30N.
做出它们的几何关系如图: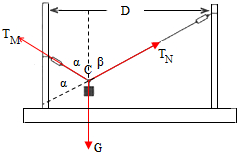
由于α=β,则:
2T0cosα=mg ①
由几何关系可知,MC与水平方向的夹角为(90°-α);
由图可知,物体的重力为3.1N.
则可知,MC与水平方向的夹角的正弦值为:sin(90°-α)=cosα=$\frac{mg}{2{T}_{0}}$=$\frac{3.1}{2×4.30}$=0.37;
故答案为:(1)100cm,TN;(2)4.3;0.37
点评 该题属于信息给予题,考查学生获取信息的能力和利用数学知识解决物理问题的能力,分析图象以及受力情况是解题的关键;本题是一道考查能力的好题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7. 如图所示,一台电动机M线圈电阻r=0.4Ω,与R=4Ω的电阻串联接在220V的电路中,电动机正常工作.已知理想电压表的示数为20V,以下说法正确的是( )
如图所示,一台电动机M线圈电阻r=0.4Ω,与R=4Ω的电阻串联接在220V的电路中,电动机正常工作.已知理想电压表的示数为20V,以下说法正确的是( )
 如图所示,一台电动机M线圈电阻r=0.4Ω,与R=4Ω的电阻串联接在220V的电路中,电动机正常工作.已知理想电压表的示数为20V,以下说法正确的是( )
如图所示,一台电动机M线圈电阻r=0.4Ω,与R=4Ω的电阻串联接在220V的电路中,电动机正常工作.已知理想电压表的示数为20V,以下说法正确的是( )| A. | 电动机的功率为1100W | |
| B. | 电动机在1分钟内做的机械功为59400J | |
| C. | 电动机在1分钟内发的热为10J | |
| D. | 整个电路在1分钟内发的热为6600J |
4. 如图所示,以8m/s匀速行驶的汽车即将通过路口,绿灯还有2s将熄灭,此时汽车距离停车线18m.该车加速时最大加速度大小为2m/s2,减速时最大加速度大小为5m/s2.此路段允许行驶的最大速度为12.5m/s,下列说法中正确的有( )
如图所示,以8m/s匀速行驶的汽车即将通过路口,绿灯还有2s将熄灭,此时汽车距离停车线18m.该车加速时最大加速度大小为2m/s2,减速时最大加速度大小为5m/s2.此路段允许行驶的最大速度为12.5m/s,下列说法中正确的有( )
 如图所示,以8m/s匀速行驶的汽车即将通过路口,绿灯还有2s将熄灭,此时汽车距离停车线18m.该车加速时最大加速度大小为2m/s2,减速时最大加速度大小为5m/s2.此路段允许行驶的最大速度为12.5m/s,下列说法中正确的有( )
如图所示,以8m/s匀速行驶的汽车即将通过路口,绿灯还有2s将熄灭,此时汽车距离停车线18m.该车加速时最大加速度大小为2m/s2,减速时最大加速度大小为5m/s2.此路段允许行驶的最大速度为12.5m/s,下列说法中正确的有( )| A. | 如果立即做匀加速运动,在绿灯熄灭前汽车可能通过停车线 | |
| B. | 如果立即做匀加速运动,在绿灯熄灭前通过停车线汽车一定超速 | |
| C. | 如果立即做匀减速运动,在绿灯熄灭前汽车能通过停车线处 | |
| D. | 如果距停车线7m处减速,汽车能停在停车线处 |
11.北京奥运会运动项目图标如图所示,形象表现出运动项目的特征,依据图标所做出的判断中,错误的是( )


| A. | 箭被射出的过程中,弹性势能转化为动能 | |
| B. | 游泳的人用力划水时,受到水的推力而前进 | |
| C. | 人举起杠铃在空中停留的几秒钟时间里,人对杠铃做了功 | |
| D. | 曲棍球的运动状态改变,是力作用的结果 |
8.平行板电容器充电后断开电源,然后将两极板间的正对面积逐渐增大,则在此过程中( )
| A. | 电容逐渐增大 | B. | 极板间场强逐渐增大 | ||
| C. | 极板间电压保持不变 | D. | 极板上电荷量变小 |