题目内容
【题目】在电荷量为Q的点电荷激发电场空间中,距Q为r处电势表达式为φ= ![]() ,其中k为静电力常量,取无穷远处为零电势点.今有一电荷量为Q的正点电荷,固定在空间中某处.一电荷量为q、质量为m的负点电荷绕其做椭圆运动,不计负点电荷重力.Q位于椭圆的一个焦点上,椭圆半长轴长为a,焦距为c,该点电荷动能与系统电势能之和表达式正确的是( )
,其中k为静电力常量,取无穷远处为零电势点.今有一电荷量为Q的正点电荷,固定在空间中某处.一电荷量为q、质量为m的负点电荷绕其做椭圆运动,不计负点电荷重力.Q位于椭圆的一个焦点上,椭圆半长轴长为a,焦距为c,该点电荷动能与系统电势能之和表达式正确的是( )
A.![]()
B.﹣ ![]()
C.﹣ ![]()
D.﹣ ![]()
【答案】B
【解析】解:如图所示,AB两点为负电荷转动中的近地点和远地点,做椭圆运动的电荷在近地点和远地点的轨道曲率半径相同,设曲率半径为r; 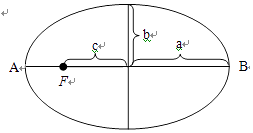
则对A点: ![]() =
= ![]()
对B点有: ![]()
则有: ![]() =
= ![]()
电荷的引力势能为EP=φq=﹣ ![]() ,动能为EK=
,动能为EK= ![]() mv2;
mv2;
则卫星在A、B两点的机械能分别为:
EA= ![]() mvA2﹣
mvA2﹣ ![]()
EB= ![]() mvB2﹣
mvB2﹣ ![]()
根据机械能守恒有:EA=EB;
联立解得:mv2A= ![]() ;mvB2=
;mvB2= ![]()
将速度分别代入,则可得出总机械能E=﹣ ![]() ,B符合题意,ACD不符合题意.
,B符合题意,ACD不符合题意.
所以答案是的:B.
【考点精析】利用万有引力定律及其应用和机械能守恒及其条件对题目进行判断即可得到答案,需要熟知应用万有引力定律分析天体的运动:把天体的运动看成是匀速圆周运动,其所需向心力由万有引力提供.即 F引=F向;应用时可根据实际情况选用适当的公式进行分析或计算.②天体质量M、密度ρ的估算;在只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目