题目内容
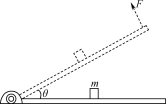
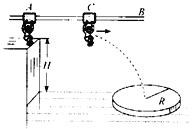
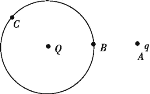
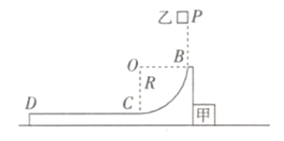
【题目】如图所示，小物块甲紧靠轨道BCD静置于光滑水平面上，轨道BCD由水平轨道CD及与CD相切于C的光滑
圆弧轨道组成，圆弧轨道的半径为R。现将小物块乙（视为质点）从B点正上方到B点高度为R的P点由静止释放，乙从B点沿切线方向进入圆弧轨道，恰好不会从水平轨道CD的左端D点掉落。已知甲、乙以及轨道BCD的质量相同，乙与CD间的动摩擦因数μ=0.5，重力加速度大小为g。求：
(1)乙通过C点时的速度大小v1；
(2)CD的长度L以及乙在CD上滑行的时间t；
(3)在乙从B点开始滑到D点的时间内，轨道BCD的位移大小x。
【答案】(1)
；(2)
，
；(3)
【解析】
(1)设乙的质量为m，当乙滑到C点时，轨道
与甲的共同速度大小为
，系统水平方向动量守恒，有
由系统机械能守恒有
解得
(2)乙滑到C点后，轨道与甲分离，设轨道与乙速度相同时的速度大小为v，乙从C点滑到D点的过程中，对乙和轨道，由动量守恒定律和能量守恒定律分别有
解得
设乙从C点滑到D点的过程中的加速度大小为a，由牛顿第二定律有
乙从C点滑到D点的过程做匀减速直线运动，有
解得
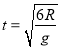
(3)设乙从B点滑到C点的时间为
，该过程轨道通过的距离为
，系统水平方向动量守恒，有
设乙沿轨道从C点运动到D点的过程中轨道通过的距离为
，由动能定理有
经分析可知
解得
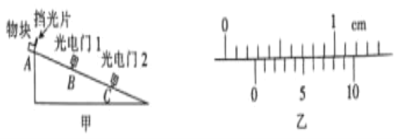
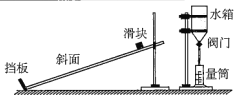
【题目】伽利略在《两种新科学的对话》一书中，讨论了自由落体运动和物体沿斜面运动的问题，提出了这样的猜想：物体沿斜面下滑是一种匀变速直线运动，同时他还运用实验验证了其猜想。物理兴趣小组依据伽利略描述的实验方案，设计了如图的装置，探究物体沿斜面下滑是否做匀变速直线运动。
（1）实验时，让滑块从某一高度由静止沿斜面下滑，并同时打开装置中的阀门，使水箱中的水流到量筒中；当滑块碰到挡板的同时关闭阀门（整个过程中水流可视为均匀稳定的）。改变滑块起始位置的高度，重复以上操作。该实验探究方案是利用量筒中收集的水量来测量________的。
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
s（m） | 4.5 | 3.9 | 3.0 | 2.1 | 1.5 | 0.9 | 0.3 |
V（mL） | 90 | 84 | 72 | 62 | 52 | 40 | 23.5 |
| 5.6 | 5.5 | 5.8 | 5.5 | 5.6 | 5.6 | 5.4 |
（2）如表是该小组测得的有关数据，其中s为滑块从斜面的不同高度由静止释放后沿斜面下滑的距离，V为相应过程量筒收集的水量。分析表中数据，根据____，可以得出滑块沿斜面下滑是做匀变速直线运动的结论。
（3）本实验误差的主要来源有：水从水箱中流出不够稳定，还可能来源于____等。（只要求写出一种）
