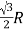Question

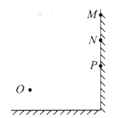
【题目】在竖直平面内，一根长为L的绝缘细线，一端固定在O点，另一端拴着质量为m、电荷量为+q的小球。小球始终处在场强大小为、方向竖直向上的匀强电场中，现将小球拉到与O点等高处，且细线处于拉直状态，由静止释放小球，当小球的速度沿水平方向时，细线被拉断，之后小球继续运动并经过P点，P点与O点间的水平距离为L。重力加速度为g，不计空气阻力，求

（1）细线被拉断前瞬间，细线的拉力大小；

（2）O、P两点间的电势差。

Answer 1

【答案】（1）FT = 1.5mg（2）

【解析】

（1）小球受到竖直向上的电场力F = qE = 1.5mg＞mg

所以小球被释放后将向上绕O点做圆周运动，到达圆周最高点时速度沿水平方向，设此时速度为v，由动能定理

设细线被拉断前瞬间的拉力为FT，由牛顿第二定律

联立解得： FT = 1.5mg

（2）细线断裂后小球做类平抛运动，加速度a竖直向上，由牛顿第二定律：F mg = ma

设细线断裂后小球经时间t到达P点，则有L = vt

小球在竖直方向上的位移为 ；解得

O、P两点沿电场方向（竖直方向）的距离为d = L + y

O、P两点间的电势差 UOP = Ed

联立解得