题目内容
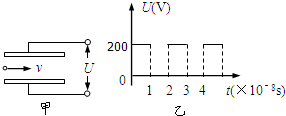
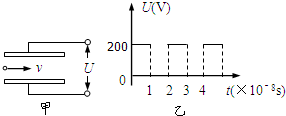
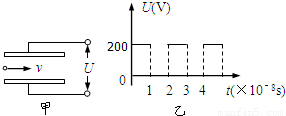
两平行金属板长L=O．1m，板间距离d=l×10-2m，从两板左端正中间有带电粒子持续飞入，如图甲所示．粒子的电量q=10-10c，质量m=10-20kg，初速度方向平行于极板，大小为v=10 7m／s，在两极板上加一按如图乙所示规律变化的电压，不计带电粒子 重力作用．求：
(1)带电粒子如果能从金属板右侧飞出，粒子在电场中运动的时间是多少?
(2)试通过计算判断在t=1．4×10-8s和t=0．6×10--8s时刻进入电场的粒子能否飞出．
解 (1)粒子在电场中飞行的时间为t则 t=L／v (1分) ．
代入数据得：．t=1×10-8S ……(1分) 。 ‘
(2)粒子在电场中运动的加速度a=Eq／m=qU／md=2 X l 0 14m／s2 ．
当t=1．4×1 O-8s时刻进入电场，考虑竖直方向运动，前０．6×1 0-8s无竖直方向位移，后0．4×10 -8s做匀加速运动。竖直方向位移 ． ’
Sy=1／2at2=0.16×10-2m<d／2=0.5×10-2m (2分)
∴能飞出两板间 (1分)
当t=O．6×1 O-8s时刻进入电场，考虑竖直方向运动，前0．4×1 0-8s匀加速运动，后O．6×1 O-8s
做匀速运动。竖直方向位移 ．
Sy'=s1+s2=1／2at2+at(T-t)=0.64 x10-2m>d／2=0.5×10-2m (2分)
∴不能飞出两板间 (1分)
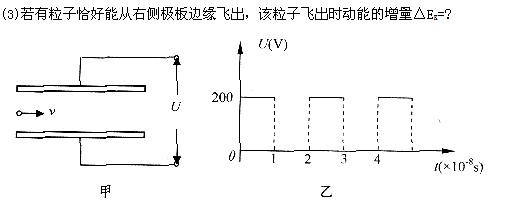
(3)若粒子恰能飞出两板间，考虑两种情况
a.竖直方向先静止再匀加速。
Sy=1／2at2 0.5×1 0-2=l／2 ×2 ×10 14t2
得t= 
／2×1 0-8s (1分)
∴ ΔEk=Uq／2=I×1 0-8J (1分)
b．竖直方向先匀加速再匀速
Sy = S1+S2 = 1／2at2 + at(T-t) 0．5 X 1 0-2=1／2X2X10 14 t2+2 X 10 14t(1×1 0-8-t)
得t = (1－√2／2)X×1 0-8S
∴S1=1／2at2 = (1．5一√2)×10-2m (1分)
∴ΔEk=EqS1=UqS1／d=(3—2√2)×1 0一8=0.1 7 X 1 0-8j (1分)
