��Ŀ����
����Ŀ����ͼΪ����̽��װ��ʾ��ͼ������I�������ΪL=0.10m���߾�ΪH=0.06m������I�ɼӷ�����ֱ���¡��糡ǿ��ΪE����ǿ�糡�������ɼӷ���ֱֽ������Ÿ�Ӧǿ��ΪB����ǿ�ų����������Ҷ˽����ſ�̽���������λ�õ���ֱ�������������������м����ٶ�v=1.0��l05m/sˮƽ���룬���Ӻ��ʱȽ���Ϊ![]() =1.0��l08C/kg�������Ա߽�ЧӦ������������
=1.0��l08C/kg�������Ա߽�ЧӦ������������
��1��������I�ӵ糡������Ӵų�ʱ������������̽�����������ӵ糡�����ֵEmax��
��2��������I���ӵ糡�������Ӵų�ʱ������������̽�����������Ӵų������ֵBmax��
��3��������I�ӵ糡EС�ڣ�1���е�Emax�������������������뿪������λ�õȸߣ���������еĴų�B������I�еĵ糡E֮��Ĺ�ϵʽ��

���𰸡���1��200N/C��2��5.5��10��3T��3��![]()
��������
(1)�����ڵ糡��������ƽ���˶����������������ֱ���˶�����ƽ���˶���ĩ�ٶȵķ����ӳ���ͨ��ˮƽ��λ�Ƶ��е㣬�����ƽ���˶��ķ��˶���ʽ��ʽ��⣻
(2) ��������ų���������Բ���˶��������ٽ�켣���õ��ٽ����뾶��Ȼ�����ţ�ٵڶ�������ʽ������
(3) �����켣����ϼ��ι�ϵ����ƽ���˶��ķ��˶���ʽ��ţ�ٵڶ�������ʽ�����������
(1) �����켣����ͼ��ʾ��
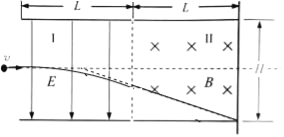
ƫת�������㣺tan��=![]()
��ֱ���ٶȣ�vy=at��
���ٶȣ�![]()
�˶�ʱ�䣺![]()
��ã�![]()
(2)�����켣����ͼ��ʾ��
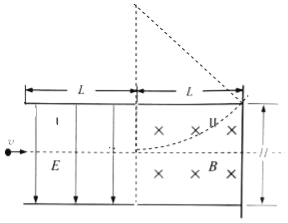
�켣Բ�뾶���㣺
![]()
��ã�![]()
Բ���˶����㣺
![]()
��ã�![]() ��
��
��3) �����켣����ͼ��ʾ��
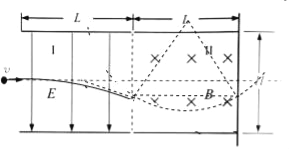
ƫת�������㣺![]()
![]()
![]()
![]()
![]()
�켣ԲԲ�Ľ�Ϊ2�����뾶���㣺
![]()
Բ���˶����㣺![]()
��ã�![]() ��
��