题目内容
16．
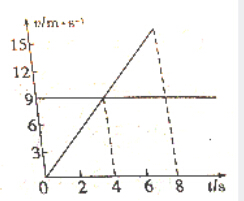A、B两质点同时经过同一点，沿同一方向做直线运动，其运动的v-t图象如图所示．则两质点再次相遇的时间t及其相遇前两者最大距离s分别是（ ）| A． | t=8s，s=12m | B． | t=8s，s=18m | C． | t=4s，s=36m | D． | t=8s，s=36m |
分析 由图可明确两物体的运动性质，则可找出二者何时相遇，何时距离最大；图象即可求得最大距离．
解答 解：物体从同一点出发，一个物体做匀速运动，另一物体做匀加速直线运动；
二者再次相遇时，经过的位移相同，即图象中图象与时间轴所围成的面积相同；则由图可知，相遇时刻为8s；
当二者速度相等时，距离最大，故4s时二者相距最远；最远距离为：s=$\frac{1}{2}$×4×9=18m；
故选：B．
点评 本题考查v-t图象的应用，要注意明确v-t图象中坐标表示速度；斜率表示加速度；而图象与时间轴所围成的面积表示位移．
练习册系列答案
相关题目
6．关于静电现象，下列说法中正确的是（ ）
| A． | 处于静电平衡状态的整个导体各处电场强度均为0 | |
| B． | 印染厂保持适当的湿度是为了防止静电 | |
| C． | 高压输电导线表面要很光滑，以避免因尖端放电而损失电能 | |
| D． | 电视机屏幕上经常有许多灰尘，这是因为电视机工作时，屏表面有静电而吸附灰尘 |
11．
如图所示水平圆半径为R，两直径AB和CD垂直，A、B、C、D四点处各分布着四个带电量均为q的正电荷，O为圆心，OP是过圆心的竖直直线．把一个带电量也为q的带正电的小球（看作点电荷）放在直线OP上的Q点，小球刚好能静止，Q点到圆心O的距离为$\sqrt{3}$R．现把此小球从Q点上方的E点静止释放，小球能运动到Q点下方的最低点F（E、F点位画出）．已知E、F两点间的距离为h，静电常数为k，重力加速度为g．则（ ）
如图所示水平圆半径为R，两直径AB和CD垂直，A、B、C、D四点处各分布着四个带电量均为q的正电荷，O为圆心，OP是过圆心的竖直直线．把一个带电量也为q的带正电的小球（看作点电荷）放在直线OP上的Q点，小球刚好能静止，Q点到圆心O的距离为$\sqrt{3}$R．现把此小球从Q点上方的E点静止释放，小球能运动到Q点下方的最低点F（E、F点位画出）．已知E、F两点间的距离为h，静电常数为k，重力加速度为g．则（ ）| A． | 小球的质量是$\frac{\sqrt{3}k{q}^{2}}{{R}^{2}g}$ | |
| B． | 直线OP上场强最大的位置一定在F点的下方 | |
| C． | 直线OP上沿O点到P点电势逐渐升高 | |
| D． | E、F两点间的电势差为UEF=-$\frac{\sqrt{3}kqh}{2{R}^{2}}$ |
12．有a、b两个粒子，质量之比是ma：mb=1：2，带电量之比是qa：qb=2：1，将a、b两个粒子从静止开始经过同一电场（ ）
| A． | 加速后a粒子的速度较大 | |
| B． | 在电场中同一点b粒子受到的电场力较大 | |
| C． | 加速后a粒子的动能较小 | |
| D． | 在电场中同一点b粒子的加速度较大 |