题目内容
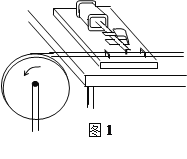
【题目】如图所示，一个电荷量为q，质量为m的带电粒子（不计重力、可为使质点），经电场加速后，小孔
射入速度选择器，恰能沿直线从小孔
射出。接着粒子垂直于AH，并从AH的中点M射入“梯形”磁场区域。最后从边界AC射出。梯形磁场区域中（含边界）磁感应强度
垂直纸面向里，大小未知， 
， 
，MN=L（
），求
（1）加速电场的加速电压；
（2）为保证粒子能从AB边射出，梯形磁场区域磁感应强度
的取值范围。
【答案】（1）
,（2）
.
【解析】试题分析：（1）加速电场运用动能定理求解，进入速度选择器电场力与洛伦兹力平衡，联立即可求出加速电场的加速电压；（2）找出粒子从AC边射出的临界条件，恰好从C点飞出和轨迹与AC边相切点恰好相切两点，利用洛伦兹力提供向心力结合临界几何关系，联立即可求出梯形磁场区域磁感应强度
的取值范围．
（1）在速度选择器中粒子做直线运动，则有： 
，解得： 
在加速电场中由动能定理可得： 
联立解得加速电压： 
（2）粒子刚好经过C点时，其运动轨迹如图所示：
由几何关系可得： 
，解得： 
粒子刚好与AC边相切时，其运动轨迹如图所示：
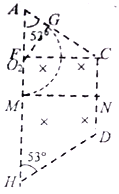
由几何关系可得： 
，解得： 
为保证粒子能从AC边射出，粒子轨迹半径r需满足： 
带电粒子在磁场中做匀速圆周运动，由牛顿第二定律： 
解得梯形磁场的磁感应强度取值范围为： 
练习册系列答案
相关题目
