题目内容
【题目】x轴下方有两个关于直线x＝－0.5a对称的沿x轴的匀强电场(大小相等，方向相反)，如图甲所示，一质量为m、带电荷量为－q的粒子(不计重力)，以初速度v沿y轴正方向从P点进入电场，后从原点O以与过P点时相同的速度进入磁场(图中未画出)，粒子过O点的同时在MN和x轴之间加上按图乙所示的规律发生周期性变化的磁场，规定垂直纸面向里为正方向，正向磁场与反向磁场的磁感应强度大小相等，且持续的时间相同，粒子在磁场中运动一段时间后到达Q点，并且速度也与过P点时速度相同，已知P、O、Q在一条直线上，与水平方向夹角为θ，且P、Q两点横坐标分别为－a、a。试计算：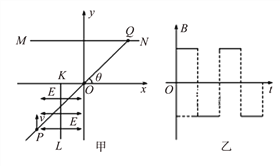
(1)电场强度E的大小。
(2)磁场的磁感应强度B的大小。
(3)粒子从P到Q的总时间。
【答案】(1) 
；(2) 
；(3) 
；
【解析】(1)带电粒子在第三象限的运动为两个阶段的匀变速曲线运动，且时间相等，设为t，对该运动分析得
y方向：atanθ＝2vt
x方向： 
解得：t＝
，E＝
。
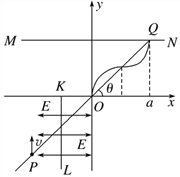
(2)带电粒子在第一象限的磁场中做匀速圆周运动，轨迹如图所示(只画出一个周期的情况)
设半径为R，由几何关系可知： 
＝4nRcosθ(n＝1,2,3，…)，
Bqv＝m
，
解得
(n＝1,2,3，…)．
(3)带电粒子在电场中运动的时间：t电＝2t＝
.
研究带电粒子在磁场中的匀速圆周运动，设时间为t磁，设单个圆弧对应的圆心角为α，由几何关系可知：α＝π－2θ，
则t磁＝2n
＝
，
所以粒子从P到Q的总时间：t总＝t电＋t磁＝
练习册系列答案
津桥教育计算小状元系列答案
相关题目
