题目内容
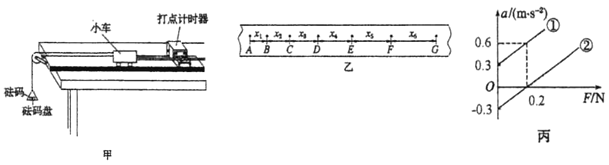
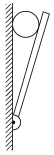
【题目】水平传送带左端与长度为L=2m的倾斜木板AB的B端紧靠,木板AB与水平方向的夹角记为θ,传送带右端与光滑半圆轨道CD的C端紧靠,圆轨道半径为R=2m;传送带左右端点间距为s=4m,其向右传输的速度为v=20m/s。质量为m=1kg的小物块与木板AB、传送带的动摩擦因数均为![]() ,小物块从木板A端以某一初速度沿木板上滑,在B端上方有一小段光滑弧,确保小物块在经过B点时,仅使运动方向变为水平,速率不变,滑上传送带,小物块继续经过传送带,冲上半圆轨道后从最高点D水平抛出。
,小物块从木板A端以某一初速度沿木板上滑,在B端上方有一小段光滑弧,确保小物块在经过B点时,仅使运动方向变为水平,速率不变,滑上传送带,小物块继续经过传送带,冲上半圆轨道后从最高点D水平抛出。
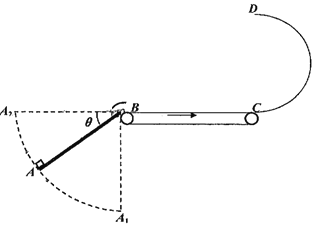
(1)若小物块自D点平抛后恰好落在传送带左端B,其速度方向与水平方向的夹角记为α,求tanα的值;
(2)若小物块以另一速度从D点平抛后落在木板A端时的速度方向与水平方向的夹角也为α,求木板AB与水平方向的夹角θ的大小;
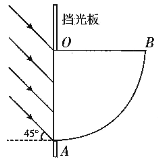
(3)若木板A端可处与1/4圆弧A1A2间的任意位置,要保证小物块都能经过D点平抛,求小物块在A端初速度的最小值.
【答案】(1)2;(2)45°;(3)10m/s。
【解析】
(1)小物块自D点平抛的时间:
![]() s
s
水平初速度:
![]() m/s
m/s
落在B点时竖直方向的速度为:
![]() m/s
m/s
则有:
![]()
(2)连接DA,设DA与水平方向的夹角为β,根据平抛运动的规律可得:
tanα=2tanβ=2
则tanβ=1
解得:
β=45°
由于s=2R=4m,所以D与B连线与水平方向的夹角为45°,可知DA连线必过B,则:
θ=β=45°;
(3)要保证小物块都能经D点平抛,在D点的最小速度为v0,则有:
![]()
根据机械能守恒定律可得:
![]()
解得物块在C点的最小速度:
![]() m/s
m/s
若物体从B到C一直加速,则B点的速度最小为vB,根据动能定理可得:
![]()
解得:
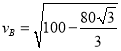 m/s
m/s
从A到B根据动能定理可得:
![]()
解得:
![]()
所以当![]() 时vA最大,则有:
时vA最大,则有:
![]()
代入数据解得:
vA=10m/s

 口算小状元口算速算天天练系列答案
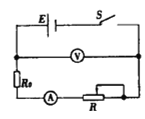
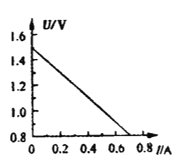
口算小状元口算速算天天练系列答案【题目】下表列出了某品牌电动自行车(如图)及所用电动机的主要技术参数,不计其自身机械损耗。若该车在额定状态下以最大运行速度行驶,则 ( )

自重 | 40(kg) | 额定电压 | 48(V) |
载重 | 75(kg) | 额定电流 | 12(A) |
最大行驶速度 | 20(km/h) | 额定输出功率 | 350(W) |
A. 电动机的输入功率为576W B. 电动机的内电阻为4Ω
C. 该车获得的牵引力为104N D. 该车受到的阻力为63N