题目内容
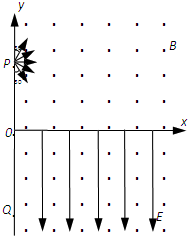 如图所示,在 xOy 平面的第一、四象限内存在着方向垂直纸面向外,磁感应强度为 B 的匀强磁场,在第四象限内存在方向沿-y 方向、电场强度为 E 的匀强电场.从 y 轴上坐标为(0,a)的 P 点向磁场区发射速度大小不等的带正电同种粒子,速度方向范围是与+y 方向成30°-150°角,且在 xOy 平面内.结果所有粒子经过磁场偏转后都垂直打到 x 轴上,然后进入第四象限内的正交电磁场区.已知带电粒子电量为+q,质量为 m,粒子重力不计.
如图所示,在 xOy 平面的第一、四象限内存在着方向垂直纸面向外,磁感应强度为 B 的匀强磁场,在第四象限内存在方向沿-y 方向、电场强度为 E 的匀强电场.从 y 轴上坐标为(0,a)的 P 点向磁场区发射速度大小不等的带正电同种粒子,速度方向范围是与+y 方向成30°-150°角,且在 xOy 平面内.结果所有粒子经过磁场偏转后都垂直打到 x 轴上,然后进入第四象限内的正交电磁场区.已知带电粒子电量为+q,质量为 m,粒子重力不计.(1)所有通过第一象限磁场区的粒子中,求粒子经历的最短时间与最长时间的比值;
(2)求粒子打到 x 轴上的范围;
(3)从 x 轴上 x=a 点射入第四象限的粒子穿过正交电磁场后从 y 轴上 y=-b 的 Q 点射出电磁场,求该粒子射出电磁场时的速度大小.
分析:(1)、先找出两个边界上的粒子,分析在第一象限内的运动情况,可知与y轴正方向成30°的粒子运动时间最长,与y轴正方向成150°的粒子运动时间最短.利用带电粒子在有边界的匀强磁场中做圆周时的时间确定方法可求出最长时间和最短时间,从而可求出时间比.
(2)、利用带电粒子在有边界的匀强磁场中做圆周运动时确定圆心和半径的方法,分别求出两种粒子经过x轴时距坐标原点的距离,从而可表示出粒子打到 x 轴上的范围.
(3)、因粒子是垂直x轴射入第四象限的,所以也是垂直于y轴射入第一象限的,由此可判断在第一象限内运动的半径为a,从而可求出射入第一象限时的速度,在第四象限内运动时,电场力做正功,使电势能转化为动能,洛伦兹力不做功,由动能定理即可求出经y轴的负方向射出第四象限时的速度.
(2)、利用带电粒子在有边界的匀强磁场中做圆周运动时确定圆心和半径的方法,分别求出两种粒子经过x轴时距坐标原点的距离,从而可表示出粒子打到 x 轴上的范围.
(3)、因粒子是垂直x轴射入第四象限的,所以也是垂直于y轴射入第一象限的,由此可判断在第一象限内运动的半径为a,从而可求出射入第一象限时的速度,在第四象限内运动时,电场力做正功,使电势能转化为动能,洛伦兹力不做功,由动能定理即可求出经y轴的负方向射出第四象限时的速度.
解答:解:
(1)、各种离子在第一象限内运动时,与y轴正方向成30°的粒子运动时间最长,时间为:
tmax=
T=
T…①
与y轴正方向成150°的粒子运动时间最短,时间为:
tmin=
T=
…②
①②两式联立得:
=
(2)、设带电粒子射入方向与y轴夹角成150°时的轨道半径为R1,由几何关系有:
R1=
= 2a
带电粒子经过的最左边为:x1=R1(1-cos30°)=(2-
)a
设带电粒子射入方向与y轴夹角30°时的轨道半径为R2,由几何关系有:
R2=
= 2a
带电粒子经过的最右边为:
x2=R2(1+cos30°)=(2+
)a
所以粒子打到 x 轴上的范围范围是:
(2-
)a≤x≤(2+
)a
(3)带电粒子在第一象限的磁场中有:
qv0B=m
由题意知:R=a
带电粒子在第四象限中运动过程中,电场力做功转化为带电粒子的动能,设经过Q点是的速度为v,由动能定理由:
qEb=
mv2-
m
解得:v=
答:(1)所有通过第一象限磁场区的粒子中,求粒子经历的最短时间与最长时间的比值为
.
(2)求粒子打到 x 轴上的范围为(2-
)a≤x≤(2+
)a.
(3)该粒子射出电磁场时的速度大小为
.
(1)、各种离子在第一象限内运动时,与y轴正方向成30°的粒子运动时间最长,时间为:
tmax=
| ||
| 2π |
| 5 |
| 12 |
与y轴正方向成150°的粒子运动时间最短,时间为:
tmin=
| ||
| 2π |
| T |
| 12 |
①②两式联立得:
| tmin |
| tmax |
| 1 |
| 5 |
(2)、设带电粒子射入方向与y轴夹角成150°时的轨道半径为R1,由几何关系有:
R1=
| a |
| sin30° |
带电粒子经过的最左边为:x1=R1(1-cos30°)=(2-
| 3 |
设带电粒子射入方向与y轴夹角30°时的轨道半径为R2,由几何关系有:
R2=
| a |
| sin30° |
带电粒子经过的最右边为:
x2=R2(1+cos30°)=(2+
| 3 |
所以粒子打到 x 轴上的范围范围是:
(2-
| 3 |
| 3 |
(3)带电粒子在第一象限的磁场中有:
qv0B=m
| ||
| R |
由题意知:R=a
带电粒子在第四象限中运动过程中,电场力做功转化为带电粒子的动能,设经过Q点是的速度为v,由动能定理由:
qEb=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
解得:v=
|
答:(1)所有通过第一象限磁场区的粒子中,求粒子经历的最短时间与最长时间的比值为
| 1 |
| 5 |
(2)求粒子打到 x 轴上的范围为(2-
| 3 |
| 3 |
(3)该粒子射出电磁场时的速度大小为
|
点评:解答本题的关键是确定带电粒子在有边界的匀强磁场中做匀速圆周运动的圆心、半径及运动时间,具体确定方法为:
①、圆心的确定:因为洛伦兹力提供向心力,所以洛伦兹力总是垂直于速度的方向,画出带电粒子运动轨迹中任意两点(一般是射入磁场和射出磁场的两点)洛伦兹力的方向,其延长线的交点即为圆心.
②、半径的确定:半径一般都是在确定圆心的基础上用平面几何的知识求解,常常用到解三角形,尤其是直角三角形.
③、运动时间的确定:利用圆心角与弦切角的关系或者四边形的内角和等于360°计算出粒子所经过的圆心角θ的大小,用公式t=
T可求出运动时间.
还有就是要明确洛伦兹力对运动电荷不做功,电场力对电荷做功的过程是电势能与动能间的互化过程.
①、圆心的确定:因为洛伦兹力提供向心力,所以洛伦兹力总是垂直于速度的方向,画出带电粒子运动轨迹中任意两点(一般是射入磁场和射出磁场的两点)洛伦兹力的方向,其延长线的交点即为圆心.
②、半径的确定:半径一般都是在确定圆心的基础上用平面几何的知识求解,常常用到解三角形,尤其是直角三角形.
③、运动时间的确定:利用圆心角与弦切角的关系或者四边形的内角和等于360°计算出粒子所经过的圆心角θ的大小,用公式t=
| θ |
| 360° |
还有就是要明确洛伦兹力对运动电荷不做功,电场力对电荷做功的过程是电势能与动能间的互化过程.

练习册系列答案
相关题目
 (2013?安徽模拟)如图所示,在xoy平面上,直线OM与x轴正方向夹角为45°,直线OM左侧存在平行y轴的匀强电场,方向沿y轴负方向.直线OM右侧存在垂直xoy平面向里的磁感应强度为B的匀强磁场.一带电量为q质量为m带正电的粒子(忽略重力)从原点O沿x轴正方向以速度vo射入磁场.此后,粒子穿过磁场与电场的边界三次,恰好从电场中回到原点O.(粒子通过边界时,其运动不受边界的影响)试求:
(2013?安徽模拟)如图所示,在xoy平面上,直线OM与x轴正方向夹角为45°,直线OM左侧存在平行y轴的匀强电场,方向沿y轴负方向.直线OM右侧存在垂直xoy平面向里的磁感应强度为B的匀强磁场.一带电量为q质量为m带正电的粒子(忽略重力)从原点O沿x轴正方向以速度vo射入磁场.此后,粒子穿过磁场与电场的边界三次,恰好从电场中回到原点O.(粒子通过边界时,其运动不受边界的影响)试求: (2011?山东模拟)如图所示,在xoy坐标平面的第一象限内有一沿y轴负方向的匀强电场,在第四象限内有一垂直于平面向里的匀强磁场.现有一粒子源处在坐标为(0,L)M点能以垂直与电场方向不断发射质量为m、电量为+q、速度为v0的粒子(重力不计),粒子进入磁场后最后又从x轴上坐标为(3L,0)处的P点射入电场,其入射方向与x轴成45°角.求:
(2011?山东模拟)如图所示,在xoy坐标平面的第一象限内有一沿y轴负方向的匀强电场,在第四象限内有一垂直于平面向里的匀强磁场.现有一粒子源处在坐标为(0,L)M点能以垂直与电场方向不断发射质量为m、电量为+q、速度为v0的粒子(重力不计),粒子进入磁场后最后又从x轴上坐标为(3L,0)处的P点射入电场,其入射方向与x轴成45°角.求: (2012?南通一模)如图所示,在xoy平面内第二象限的某区域存在一个矩形匀强磁场区,磁场方向垂直xoy平面向里,边界分别平行于x轴和y轴.一电荷量为e、质量为m的电子,从坐标原点O以速度v0射入第二象限,速度方向与y轴正方向成45°角,经过磁场偏转后,通过P(0,a)点,速度方向垂直于y轴,不计电子的重力.
(2012?南通一模)如图所示,在xoy平面内第二象限的某区域存在一个矩形匀强磁场区,磁场方向垂直xoy平面向里,边界分别平行于x轴和y轴.一电荷量为e、质量为m的电子,从坐标原点O以速度v0射入第二象限,速度方向与y轴正方向成45°角,经过磁场偏转后,通过P(0,a)点,速度方向垂直于y轴,不计电子的重力. 如图所示,在xOy坐标系中以O为中心的椭圆上有M、C、P、N、D五个点,现在其一个焦点A上放一正点电荷,则下列判断正确的是( )
如图所示,在xOy坐标系中以O为中心的椭圆上有M、C、P、N、D五个点,现在其一个焦点A上放一正点电荷,则下列判断正确的是( ) 如图所示,在xOy平面的第Ⅱ象限内有半径为R的圆分别与x轴、y轴相切于P、Q 两点,圆内存在垂直于xOy平面向外的匀强磁场.在第I象限内存在沿y轴负方向的匀强电场,电场强度为E,一带正电的粒子(重力不计)以速率v0从P点射入磁场后恰好垂直y轴进入电场,最后从M(
如图所示,在xOy平面的第Ⅱ象限内有半径为R的圆分别与x轴、y轴相切于P、Q 两点,圆内存在垂直于xOy平面向外的匀强磁场.在第I象限内存在沿y轴负方向的匀强电场,电场强度为E,一带正电的粒子(重力不计)以速率v0从P点射入磁场后恰好垂直y轴进入电场,最后从M(