题目内容

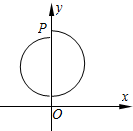
（2012?南通一模）如图所示，在xoy平面内第二象限的某区域存在一个矩形匀强磁场区，磁场方向垂直xoy平面向里，边界分别平行于x轴和y轴．一电荷量为e、质量为m的电子，从坐标原点O以速度v0射入第二象限，速度方向与y轴正方向成45°角，经过磁场偏转后，通过P（0，a）点，速度方向垂直于y轴，不计电子的重力．
（1）若磁场的磁感应强度大小为B0，求电子在磁场中的运动时间t；
（2）为使电子完成上述运动，求磁感应强度B的大小应满足的条件；
（3）若电子到达y轴上P点时，撤去矩形匀强磁场，同时在y轴右侧加方向垂直xoy平面向里的匀强磁场，磁感应强度大小为B1，在y轴左侧加方向垂直xoy平面向里的匀强磁场，电子在第（k+1）次从左向右经过y轴（经过P点为第1次）时恰好通过坐标原点，求y轴左侧磁场磁感应强度的大小B2及上述过程电子的运动时间t．
分析：（1）电子在磁场中由洛伦兹力提供向心力而做匀速圆周运动，确定电子圆周运动的圆心角，由t=
θ
2π
T求出时间t；
（2）当磁感应强度最小时，电子回旋半径最大，由几何知识求出最大半径，即可求得B的最小值，从而可求得磁感应强度B的大小应满足的条件．
（3）由几何知识求得电子在y轴右侧和左侧做圆周运动的半径与a的关系，即可求出B2．并求出时间．
解答：解：（1）如图甲所示，电子在磁场中转过的角度θ=
3π
4

运动周期  T=
2πm
eB0

则电子在磁场中的运动时间t=
θ
2π
T
解得  t=
3πm
4eB0

（2）设磁感应强度最小值为Bmin，对应最大回旋半径为R，圆心O1，则有
   ev0Bmin=
m
v
2
0
R

由几何关系得 R+
2
R=a
解得  Bmin=
(
2
+1)mv0
ea

则磁感应强度B应满足的条件为  B≥
(
2
+1)mv0
ea

（3）设电子在y轴右侧和左侧做圆周运动的半径分别为r1和r2，则有ev0B1=
m
v
2
0
r1
，ev0B2=
m
v
2
0
r2

如图乙的几何关系可知2k（r1-r2）=a
解得  B2=
2kmv0B1
2kmv0-aeB1

设电子在y轴右侧和左侧做圆周运动的周期分别为T1和T2，则
  T1=
2πm
eB1
，
  T2=
2πm
eB2
t=k?
T1+T2
2

解得  t=
2kπm
eB1
-
πa
2v0

解：
（1）若磁场的磁感应强度大小为B0，电子在磁场中的运动时间t是
3πm
4eB0
；
（2）为使电子完成上述运动，磁感应强度B的大小应满足的条件是 B≥
(
2
+1)mv0
ea
；
（3）y轴左侧磁场磁感应强度的大小B2为
2kmv0B1
2kmv0-aeB1
，上述过程电子的运动时间t为
2kπm
eB1
-
πa
2v0
．
点评：本题的解题关键是根据几何知识求出电子回旋的最大半径，根据圆心角，由t=
θ
2π
T求时间是常用的方法，要熟练掌握．
练习册系列答案
相关题目
（2012?南通一模）2012年2月25日凌晨，我国成功地将第十一颗北斗导航卫星送入太空预定转移轨道，它最终将被定点成为一颗地球静止轨道卫星，则（　　）
（2012?南通一模）将一小球从高处水平抛出，最初2s内小球动能Ek随时间t变化的图线如图所示，不计空气阻力，重力加速度g=10m．s2．根据图象信息，不能确定的物理量是（　　）
（2012?南通一模）自由中子是不稳定的，它的平均寿命大约是900s，它能自发地发生放射性衰变，衰变方程是：
 
1
0
n→
 
1
1
H+X+
.
v
e，其中
.
v
e是反电子中微子（不带电的质量很小的粒子）．下列说法中正确的是 （　　）
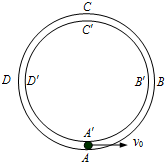（2012?南通二模）如图所示，在竖直平面内固定有两个很靠近的同心圆形轨道，外圆ABCD的光滑，内圆A′B′C′D′的上半部分B′C′D′粗糙，下半部分B′A′D′光滑．一质量m=0.2kg的小球从轨道的最低点A，以初速度v0向右运动，球的尺寸略小于两圆间距，球运动的半径R=0.2m，取g=10m/s2．
（1）若要使小球始终紧贴外圆做完整的圆周运动，初速度v0至少为多少？
（2）若v0=3m/s，经过一段时间小球到达最高点，内轨道对小球的支持力N=2N，则小球在这段时间内克服摩擦力做的功是多少？
（3）若v0=3m/s，经过足够长的时间后，小球经过最低点A时受到的支持力为多少？小球在整个运动过程中减少的机械能是多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网