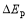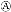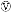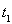Question

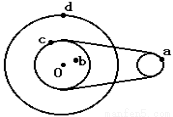
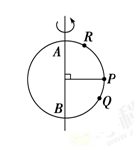
如图所示，一圆环以直径AB为轴做匀速转动，P、Q、R是环上的三点，则下列说法正确的是（ ）

A．向心加速度的大小aP＝aQ＝aR

B．任意时刻P、Q、R三点向心加速度的方向不同

C．线速度vP>vQ>vR

D．任意时刻P、Q、R三点的线速度方向均不同

 

Answer 1

C

【解析】

试题分析: 一圆环以直径AB为轴做匀速转动，圆环上各点角速度相等，根据公式an=ω2r，向心加速度与到转动轴O的距离成正比，aP＞aQ＞aR，故A错误；三点向心加速度的方向均是水平指向AB轴的，可以看出任意时刻P、Q、R三点向心加速度的方向相同，故B错误；由图可知：半径rP＞rQ＞rR，由v=ωr可知，角速度相等，线速度vP＞vQ＞vR，故C正确；线速度的方向为该点的切线方向，任意时刻P、Q、R三点的线速度方向均相同，故D错误；

考点：向心力