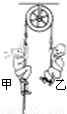
题目内容
如图所示为阿特伍德设计的装置，不考虑绳与滑轮的质量，不计轴承摩擦、绳与滑轮间的摩擦．初始时两人均站在水平地面上；当位于左侧的甲用力向上攀爬时，位于右侧的乙始终用力抓住绳子，最终至少一人能到达滑轮．下列说法正确的是（ ）
| A．若甲的质量较大，则乙先到达滑轮 |
| B．若甲的质量较大，则甲、乙同时到达滑轮 |
| C．若甲、乙质量相同，则乙先到达滑轮 |
| D．若甲、乙质量相同，则甲先到达滑轮 |
对甲有：F-mAg=mAaA，解得aA=
=
-g，对乙有：F-mBg=mBaB，解得：
aB=
=
-g．
当甲的质量大，则甲的加速度小，根据l=
at2知，甲的运动时间长，所以乙先到达滑轮．
当甲乙的质量相等，则运动时间相同，同时到达滑轮．故A正确，B、C、D错误．
故选A．
| F-mAg |
| mA |
| F |
| mA |
aB=
| F-mBg |
| mB |
| F |
| mB |
当甲的质量大，则甲的加速度小，根据l=
| 1 |
| 2 |
当甲乙的质量相等，则运动时间相同，同时到达滑轮．故A正确，B、C、D错误．
故选A．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
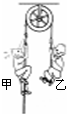如图所示为阿特伍德设计的装置，不考虑绳与滑轮的质量，不计轴承摩擦、绳与滑轮间的摩擦．初始时两人均站在水平地面上；当位于左侧的甲用力向上攀爬时，位于右侧的乙始终用力抓住绳子，最终至少一人能到达滑轮．下列说法正确的是（ ）
