题目内容
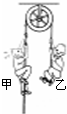
如图所示为阿特伍德设计的装置,不考虑绳与滑轮的质量,不计轴承摩擦、绳与滑轮间的摩擦.初始时两人均站在水平地面上;当位于左侧的甲用力向上攀爬时,位于右侧的乙始终用力抓住绳子,最终至少一人能到达滑轮.下列说法正确的是( )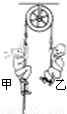
A.若甲的质量较大,则乙先到达滑轮
B.若甲的质量较大,则甲、乙同时到达滑轮
C.若甲、乙质量相同,则乙先到达滑轮
D.若甲、乙质量相同,则甲先到达滑轮
【答案】分析:不管怎么拉,绳子对两人的拉力大小相等,根据牛顿第二定律比较出加速度的大小,从而根据位移时间公式进行判断.
解答:解:对甲有:F-mAg=mAaA,解得 ,对乙有:F-mBg=mBaB,解得:
,对乙有:F-mBg=mBaB,解得:
 .
.
当甲的质量大,则甲的加速度小,根据l= 知,甲的运动时间长,所以乙先到达滑轮.
知,甲的运动时间长,所以乙先到达滑轮.
当甲乙的质量相等,则运动时间相同,同时到达滑轮.故A正确,B、C、D错误.
故选A.
点评:解决本题的关键抓住绳子拉力大小相等,结合牛顿第二定律和运动学公式进行求解.
解答:解:对甲有:F-mAg=mAaA,解得
 ,对乙有:F-mBg=mBaB,解得:
,对乙有:F-mBg=mBaB,解得: .
.当甲的质量大,则甲的加速度小,根据l=
 知,甲的运动时间长,所以乙先到达滑轮.
知,甲的运动时间长,所以乙先到达滑轮.当甲乙的质量相等,则运动时间相同,同时到达滑轮.故A正确,B、C、D错误.
故选A.
点评:解决本题的关键抓住绳子拉力大小相等,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
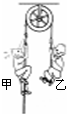 如图所示为阿特伍德设计的装置,不考虑绳与滑轮的质量,不计轴承摩擦、绳与滑轮间的摩擦.初始时两人均站在水平地面上;当位于左侧的甲用力向上攀爬时,位于右侧的乙始终用力抓住绳子,最终至少一人能到达滑轮.下列说法正确的是( )
如图所示为阿特伍德设计的装置,不考虑绳与滑轮的质量,不计轴承摩擦、绳与滑轮间的摩擦.初始时两人均站在水平地面上;当位于左侧的甲用力向上攀爬时,位于右侧的乙始终用力抓住绳子,最终至少一人能到达滑轮.下列说法正确的是( )