题目内容
1.某人造卫星绕地球做匀速圆周运动,它离地面的高度为h,地球半径为R,地球表面的重力加速度为g.不考虑地球自转的影响.求:(1)推导地球的第一宇宙速度v1的表达式
(2)卫星的线速度大小.
分析 人造卫星绕地球做匀速圆周运动,由万有引力充当向心力,对地球表面的物体,根据万有引力等于重力,联立解得卫星的线速度大小.
解答 解:(1)根据题给条件由万有引力充当向心力:$\frac{GMm}{{R}^{2}}=m\frac{{V}_{1}}{R}$
得:V1=$\sqrt{gR}$
(2)设地球质量为M,卫星质量为m,引力常量为G.
根据牛顿第二定律,得:$G\frac{Mm}{{{{(R+h)}^2}}}=m\frac{v^2}{R+h}$
地球表面处物体所受万有引力近似等于重力,即$G\frac{Mm}{R^2}=mg$解得;$v=\sqrt{\frac{{{R^2}g}}{R+h}}$
答:(1)推导地球的第一宇宙速度$\sqrt{gR}$(2)卫星的线速度大小$v=\sqrt{\frac{{{R^2}g}}{R+h}}$
点评 人造地球卫星所受到的万有引力充当向心力,地球表面的物体受到的重力等于万有引力,这两个关系是解决天体问题的重要的两个关系,一定要熟练掌握

练习册系列答案
相关题目
14. 如图所示,民族运动会上运动员骑马沿着跑道AB运动,同时拉弓放箭射向靶子.假设马奔驰的速度为v1,运动员静止时射出的箭的速度为v2,跑道距离靶子的最近距离OA=d.不计空气阻力,要想命中目标且箭在空中飞行时间最短,则( )
如图所示,民族运动会上运动员骑马沿着跑道AB运动,同时拉弓放箭射向靶子.假设马奔驰的速度为v1,运动员静止时射出的箭的速度为v2,跑道距离靶子的最近距离OA=d.不计空气阻力,要想命中目标且箭在空中飞行时间最短,则( )
 如图所示,民族运动会上运动员骑马沿着跑道AB运动,同时拉弓放箭射向靶子.假设马奔驰的速度为v1,运动员静止时射出的箭的速度为v2,跑道距离靶子的最近距离OA=d.不计空气阻力,要想命中目标且箭在空中飞行时间最短,则( )
如图所示,民族运动会上运动员骑马沿着跑道AB运动,同时拉弓放箭射向靶子.假设马奔驰的速度为v1,运动员静止时射出的箭的速度为v2,跑道距离靶子的最近距离OA=d.不计空气阻力,要想命中目标且箭在空中飞行时间最短,则( )| A. | 箭射到靶的最短时间为$\frac{d}{{v}_{2}}$ | |
| B. | 箭射到靶的最短时间为$\frac{d}{\sqrt{{{v}_{2}}^{2}-{{v}_{1}}^{2}}}$ | |
| C. | 运动员应在到达A点前瞄准靶心放箭 | |
| D. | 运动员应在到达A点时瞄准靶心放箭 |
9.一名宇航员来到一个星球上,如果该星球的质量是地球质量的一半,它的直径也是地球直径的一半,那么这名宇航员在该星球上所受的万有引力大小是他在地球上所受万有引力大小的( )
| A. | 0.25倍 | B. | 0.5倍 | C. | 2倍 | D. | 4倍 |
6.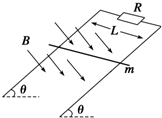 如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动.导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g.下列选项正确的是( )
如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动.导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g.下列选项正确的是( )
 如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动.导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g.下列选项正确的是( )
如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动.导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g.下列选项正确的是( )| A. | P=2mgvsin θ | |
| B. | P=3mgvsin θ | |
| C. | 当导体棒速度达到$\frac{v}{2}$时加速度大小为$\frac{g}{2}$sin θ | |
| D. | 在速度达到2v以后匀速运动的过程中,R上产生的焦耳热等于拉力所做的功 |
10.下列说法正确的是( )
| A. | 物体吸收热量,其温度一定升高 | |
| B. | 做功和热传递是改变物体内能的两种方式 | |
| C. | 布朗运动是悬浮在液体中固体颗粒的分子无规则运动的反映 | |
| D. | 第二类永动机是不能制造出来的,尽管它不违反热力学第一定律,但它违反热力学第二定律 |
 两个天体(包括人造天体)间存在万有引力,并具有由相对位置决定的势能.如果两个天体的质量分别为m1和m2,当它们相距无穷远时势能为零,则它们距离为r时,引力势能为EP=-G$\frac{{m}_{1}{m}_{2}}{r}$.发射地球同步卫星一般是把它先送入较低的圆形轨道,如图中Ⅰ,再经过两次“点火”,即先在图中a点处启动燃气发动机,向后喷出高压燃气,卫星得到加速,进入图中的椭圆轨道Ⅱ,在轨道Ⅱ的远地点b处第二次“点火”,卫星再次被加速,此后,沿图中的圆形轨道Ⅲ(即同步轨道)运动.设某同步卫星的质量为m,地球半径为R,轨道Ⅰ距地面非常近,轨道Ⅲ距地面的距离近似为6R,地面处的重力加速度为g,并且每次点火经历的时间都很短,点火过程中卫星的质量减少可以忽略.求:
两个天体(包括人造天体)间存在万有引力,并具有由相对位置决定的势能.如果两个天体的质量分别为m1和m2,当它们相距无穷远时势能为零,则它们距离为r时,引力势能为EP=-G$\frac{{m}_{1}{m}_{2}}{r}$.发射地球同步卫星一般是把它先送入较低的圆形轨道,如图中Ⅰ,再经过两次“点火”,即先在图中a点处启动燃气发动机,向后喷出高压燃气,卫星得到加速,进入图中的椭圆轨道Ⅱ,在轨道Ⅱ的远地点b处第二次“点火”,卫星再次被加速,此后,沿图中的圆形轨道Ⅲ(即同步轨道)运动.设某同步卫星的质量为m,地球半径为R,轨道Ⅰ距地面非常近,轨道Ⅲ距地面的距离近似为6R,地面处的重力加速度为g,并且每次点火经历的时间都很短,点火过程中卫星的质量减少可以忽略.求: 在现代化的钢铁厂中,一般采用滚筒传送钢锭.如图所示为我国某钢铁厂的钢锭传送装置,斜坡长L=20m,高h=2m,斜坡上紧排着一排滚筒.长l=8m、质量m=1.0×103kg的钢锭ab放在滚筒上,钢锭与滚筒间的动摩擦因数μ=0.3,工作时由电动机带动所有滚筒顺时针匀速转动,使钢锭沿斜坡向上移动,滚筒边缘的线速度大小均为v=4m/s.由于斜坡倾角很小,可认为钢锭对滚筒的总压力近似等于钢锭的重力.取当地重力加速度g=10m/s2.
在现代化的钢铁厂中,一般采用滚筒传送钢锭.如图所示为我国某钢铁厂的钢锭传送装置,斜坡长L=20m,高h=2m,斜坡上紧排着一排滚筒.长l=8m、质量m=1.0×103kg的钢锭ab放在滚筒上,钢锭与滚筒间的动摩擦因数μ=0.3,工作时由电动机带动所有滚筒顺时针匀速转动,使钢锭沿斜坡向上移动,滚筒边缘的线速度大小均为v=4m/s.由于斜坡倾角很小,可认为钢锭对滚筒的总压力近似等于钢锭的重力.取当地重力加速度g=10m/s2. 如图所示,一个挂在绝缘细线下端的带正电的小球B,静止在图示位置,若固定的带正电的小球A的电荷量为Q,B球的质量为m,带电荷量为q,θ=30°,A和B在同一条水平线上,整个装置处于真空中.求:
如图所示,一个挂在绝缘细线下端的带正电的小球B,静止在图示位置,若固定的带正电的小球A的电荷量为Q,B球的质量为m,带电荷量为q,θ=30°,A和B在同一条水平线上,整个装置处于真空中.求: