题目内容
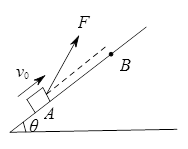
（9分）如图甲所示，有一足够长的粗糙斜面，倾角θ＝37°，一滑块以初速度v0＝16 m/s从底端A点滑上斜面，滑至B点后又返回到A点．滑块运动的图象如图乙所示，求：（已知：sin37°＝0.6，cos 37°＝0.8，重力加速度g＝10 m/s2）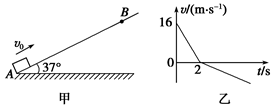
（1）AB之间的距离；
（2）滑块再次回到A点时的速度；
（3）滑块在整个运动过程中所用的时间。
（1）16m （2）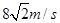
（3）（2＋2
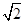）s
解析试题分析：⑴ 由v-t图像知AB之间的距离为0－2s内图像与坐标轴围成的面积为：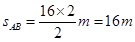
⑵ 设滑从A滑到B过程的加速度大小为a1,从B返回A过程的加速度大小为a2,滑块与斜面间的动摩擦因数为μ ，根据牛顿第二定律则：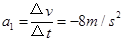
a2=gsinθ-μgcosθ
设滑块返回到A点时的速度为v2,根据：
联立以上各式解得：a2=4m/s2，v2=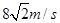
⑶，设滑块从A到B的时间为t1,从B返回到A用时t2,
则有：t1＝2 s，t2＝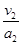
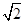＝2s
则滑块在整个运动过程中所用的时间为
t＝t1＋t2＝（2＋2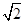）s
考点：本题考查牛顿运动定律、匀变速直线运动规律。
练习册系列答案
相关题目
；
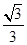。（重力加速度g取10 m/s2） 
