题目内容
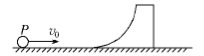
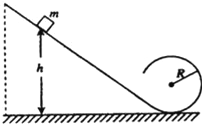
【题目】如图所示，位于竖直平面内的光滑轨道，由一段斜的直轨道与之相切的圆形轨道连接而成，圆形轨道的半径为R．一质量为m的小物块从斜轨道上某处由静止开始下滑，然后沿圆形轨道运动．要求物块能通过圆形轨道最高点，且在该最高点与轨道间的压力不能超过5mg（g为重力加速度）．求物块初始位置相对于圆形轨道底部的高度h的取值范围．
【答案】
【解析】试题分析：要求物块相对于圆轨道底部的高度，必须求出物块到达圆轨道最高点的速度，在最高点，物体做圆周运动的向心力由重力和轨道对物体的压力提供，当压力恰好为0时，h最小；当压力最大时，h最大．由机械能守恒定律和牛顿第二定律结合解答。
设物块在圆形轨道最高点的速度为v，由机械能守恒得：
物块在最高点受的力为重力mg，轨道的压力
,重力与压力的合力提供向心力，有
物块能通过最高点的条件是
由以上式得
联立以上各式得
根据题目要求
由以上各式得
由此可得
所以h的取值范围是
练习册系列答案
目标测试系列答案
相关题目
【题目】下表列出了某品牌电动自行车(如图)及所用电动机的主要技术参数，不计其自身机械损耗。若该车在额定状态下以最大运行速度行驶，则 ( )
自重 | 40(kg) | 额定电压 | 48(V) |
载重 | 75(kg) | 额定电流 | 12(A) |
最大行驶速度 | 20(km/h) | 额定输出功率 | 350(W) |
A. 电动机的输入功率为576W B. 电动机的内电阻为4Ω
C. 该车获得的牵引力为104N D. 该车受到的阻力为63N