题目内容
15. 如图所示,P是倾角为30°的光滑固定斜面.劲度系数为k的轻弹簧一端固定在斜面底端的固定挡板C上,另一端与质量 物块A相连接.细绳另一端系物体A上,细绳跨过不计质量和摩擦的定滑轮,另有一个不计质量的小挂钩,小挂钩不挂任何物体时,物体A处于静止状态,细绳与斜面平行.小挂钩上轻轻挂上一个质量也为m物块B后,物体A沿斜面向上运动,斜面足够长,运动过程中物块B始终未接触地面.已知重力加速度为g=10m/s2
如图所示,P是倾角为30°的光滑固定斜面.劲度系数为k的轻弹簧一端固定在斜面底端的固定挡板C上,另一端与质量 物块A相连接.细绳另一端系物体A上,细绳跨过不计质量和摩擦的定滑轮,另有一个不计质量的小挂钩,小挂钩不挂任何物体时,物体A处于静止状态,细绳与斜面平行.小挂钩上轻轻挂上一个质量也为m物块B后,物体A沿斜面向上运动,斜面足够长,运动过程中物块B始终未接触地面.已知重力加速度为g=10m/s2(1)求小挂钩不挂任何物体时弹簧的压缩量为x1
(2)设物块A沿斜面上升通过Q点位置时速度最大,求Q点到出发点距离x0及最大速vm;
(3)把物块B质量变为nm(n>0.5),小明同学认为,只要n足够大,就可以使物块A沿斜面上滑到Q点时速度增大到2vm,你认为是否正确?如果正确,请说明理由,如果不正确,请求出A沿斜面上升到Q点位置时速度范围.
分析 (1)小挂钩不挂任何物体时,物体A处于静止状态,由平衡条件求出弹簧的形变量;
(2)当A受到的合力为零时速度最大,根据平衡条件求出形变量,再由机械能守恒定律可以求出最大速度.
(3)由机械能守恒定律求出A的速度,然后求出速度的大小范围.
解答 解:(1)小挂钩不挂任何物体时,物体A处于静止状态,由平衡条件得:mgsin30°=kx,
得:x=$\frac{mg}{2k}$,
(2)当A受到的合力为零时速度最大,此时:
mgsin30°+kx′=mg,
解得:x=x′=$\frac{mg}{2k}$,
Q点到出发点的距离:x0=2x=$\frac{mg}{k}$;
在出发点与Q弹簧的形变量相同,弹簧的弹性势能相等,
由机械能守恒定律得:mgx0=mgx0sin30°+$\frac{1}{2}$•2mv2,
解得,最大速度:vm=g$\sqrt{\frac{m}{2k}}$;
(4)B的质量变为nm时,由机械能守恒定律得:
nmgx0=mgx0sin30°+$\frac{1}{2}$•(nm+m)v2,
解得:v=g$\sqrt{\frac{m(2n-1)}{k(n+1)}}$,
n→∞时,v=g$\sqrt{\frac{2m}{k}}$=2vm,
由于n不会达到无穷大,因此速度不会达到2vm,
小明的说法是错误的,速度范围是:0<v<g$\sqrt{\frac{2m}{k}}$.
答:(1)小挂钩不挂任何物体时弹簧的压缩量为x1为$\frac{mg}{2k}$;
(2)设物块A沿斜面上升通过Q点位置时速度最大,Q点到出发点距离为$\frac{mg}{k}$,最大速为g$\sqrt{\frac{m}{2k}}$;
(3)小明的观点错误,A沿斜面上升到Q点位置时速度范围为0<v<g$\sqrt{\frac{2m}{k}}$.
点评 本题考查牛顿第二定律的应用及机械能守恒定律;要分析清楚物体的运动过程,应用牛顿第二定律与机械能守恒定律可以正确解题,难度适中.


| A. | A、D两点场强大小相等,方向相反 | B. | E、O、F三点比较,O点电势最高 | ||
| C. | E、O、F三点比较,O点场强最强 | D. | B、O、C三点比较,O点场强最强 |

| A. | 去掉单缝S,屏上无干涉条纹 | |
| B. | 去掉双缝C,屏上将无任何条纹 | |
| C. | 用不同颜色的透明玻璃分别遮住S1、S2,屏上将无任何干涉条纹 | |
| D. | 无论普通光源频率如何变化,屏中央O处始终为亮条纹 |
| A. | 光子与光电子是同一种粒子 | |
| B. | 光子与物质微粒发生相互作用时,不仅遵循能量守恒,还遵循动量守恒 | |
| C. | 光具有粒子性又具有波动性,这种波是概率波,不是电磁波 | |
| D. | 宏观物体也有波动性,这种波就是机械波 |
 如图所示,平行光滑导轨倾斜放置,与水平面的夹角为60°,质量为m的导体棒ab静止在平行导轨上,导轨宽度为L,已知电源的电动势为E,内阻为r,导体棒的电阻为R,其余接触电阻不计,磁场方向竖直向上.
如图所示,平行光滑导轨倾斜放置,与水平面的夹角为60°,质量为m的导体棒ab静止在平行导轨上,导轨宽度为L,已知电源的电动势为E,内阻为r,导体棒的电阻为R,其余接触电阻不计,磁场方向竖直向上.
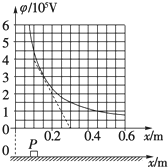 粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,且沿x轴方向的电势φ与坐标值x的关系如图所示,即φ-x图象是一条反比例函数图线.现有一质量为0.10kg、电荷量为1.0×10-7 C带正电荷的滑块(可视为点电荷)沿着x轴运动,滑块与水平面的动摩擦因数为0.20,重力加速度g=10m/s2.
粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,且沿x轴方向的电势φ与坐标值x的关系如图所示,即φ-x图象是一条反比例函数图线.现有一质量为0.10kg、电荷量为1.0×10-7 C带正电荷的滑块(可视为点电荷)沿着x轴运动,滑块与水平面的动摩擦因数为0.20,重力加速度g=10m/s2.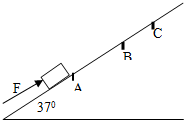 如图所示,一小木块在沿倾角为370的斜面上受沿斜面向上的恒定外力F作用,从A点由静止开始做匀加速运动,前进4m到达B点,速度达到8m/s,木块与斜面间的动摩擦因数μ=0.5,木块质量m=1kg.(g=10m/s2,Sin37°=0.6,cos37°=0.8 ).求:
如图所示,一小木块在沿倾角为370的斜面上受沿斜面向上的恒定外力F作用,从A点由静止开始做匀加速运动,前进4m到达B点,速度达到8m/s,木块与斜面间的动摩擦因数μ=0.5,木块质量m=1kg.(g=10m/s2,Sin37°=0.6,cos37°=0.8 ).求: