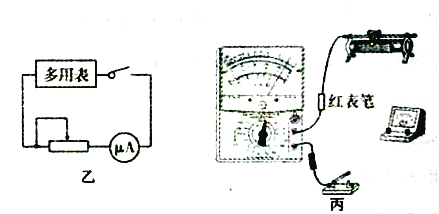
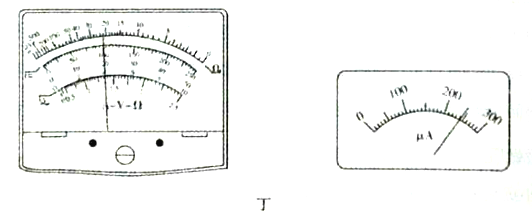
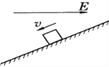
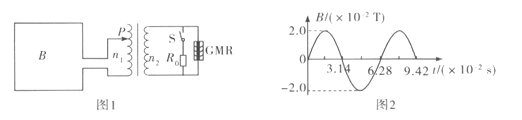题目内容
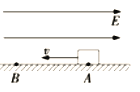
【题目】把一个质量为![]() 、带正电荷且电量为
、带正电荷且电量为![]() 的小物块放在一个水平轨道的
的小物块放在一个水平轨道的![]() 点上,在轨道的
点上,在轨道的![]() 点有一面与轨道垂直的固定墙壁.轨道处于匀强电场中,电场强度的大小为
点有一面与轨道垂直的固定墙壁.轨道处于匀强电场中,电场强度的大小为![]() ,其方向与轨道(
,其方向与轨道(![]() 轴)平行且方向向左.若把小物块
轴)平行且方向向左.若把小物块![]() 从静止状态开始释放,它能够沿着轨道滑动.已知小物块
从静止状态开始释放,它能够沿着轨道滑动.已知小物块![]() 与轨道之间的动摩擦因数
与轨道之间的动摩擦因数![]() ,
, ![]() 点到墙壁的距离为
点到墙壁的距离为![]() ,若
,若![]() 与墙壁发生碰撞时,其电荷
与墙壁发生碰撞时,其电荷![]() 保持不变,而且碰撞为完全弹性碰撞(不损失机械能).求:
保持不变,而且碰撞为完全弹性碰撞(不损失机械能).求:
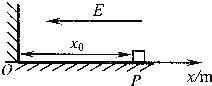
(1)如果在![]() 点把小物块从静止状态开始释放,那么它第
点把小物块从静止状态开始释放,那么它第![]() 次撞墙后瞬时速度为零的位置坐标
次撞墙后瞬时速度为零的位置坐标![]() 的表达式分别是什么?
的表达式分别是什么?
(2)如果在![]() 点把小物块从静止状态开始释放,那么它最终会停留在什么位置?从开始到最后它一共走了多少路程(
点把小物块从静止状态开始释放,那么它最终会停留在什么位置?从开始到最后它一共走了多少路程(![]() )?
)?
(3)如果在![]() 点瞬间给小物块一个沿着
点瞬间给小物块一个沿着![]() 轴向右的初始冲量,其大小设为
轴向右的初始冲量,其大小设为![]() ,那么它第一次又回到
,那么它第一次又回到![]() 点时的速度(
点时的速度(![]() )大小为多少?它最终会停留在什么位置?从开始到最后它一共走了多少路程(
)大小为多少?它最终会停留在什么位置?从开始到最后它一共走了多少路程(![]() )?
)?
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
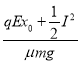
【解析】试题分析:(1)分析滑块在水平方向的受力情况,根据功能关系列式分别求出速度为零的位置坐标.(2)由于克服摩擦力做功,滑块的机械能不断减小,最终停在O点,对全过程运用功能关系列式,求总路程.滑动摩擦力做功与总路程有关.(3)由动量定理得到滑块获得的初速度,再运用功能关系列式,求出第一次又回到P点时的速度大小,确定出最终停止的位置,对整个过程,由功能关系求总路程.
(1)根据题意分析知,小物块![]() 沿着轨道滑动时,水平方向上受到二力:滑动摩擦力
沿着轨道滑动时,水平方向上受到二力:滑动摩擦力![]() 和电场力
和电场力![]() ,而且总有:
,而且总有: ![]()
取墙面为零电势面,则在这一运动过程中应用功能关系有: ![]()
联立得: ![]()
(2)它最终会停留在![]() 点,对从开始到最终的整个运动过程应用功能关系有:
点,对从开始到最终的整个运动过程应用功能关系有: ![]()
解得: ![]()
(3)由动量定理知,小物块获得一个向右的初始冲量![]() ,那么向右运动的初速度:
,那么向右运动的初速度: ![]()
设第一次瞬时速度为零的位置坐标为![]() 取墙面为零电势面,则在这一运动中应用功能关系有:
取墙面为零电势面,则在这一运动中应用功能关系有: ![]()
得: 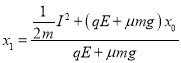
同上道理,对从开始互第一次又回到![]() 点,这一过程应用功能关系有:
点,这一过程应用功能关系有: ![]()
解得: ![]()
又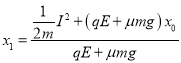
解得: ![]()
小物块最终会停留在![]() 点,设从开始到最后一共走的路程为
点,设从开始到最后一共走的路程为![]() ,全过程应用功能关系有:
,全过程应用功能关系有: ![]()
解得: 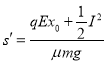

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案