题目内容
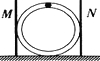
【题目】如图所示,内壁光滑的圆管形轨道竖直放置在光滑水平地面上,且恰好处在两固定光滑挡板M、N之间,圆轨道半径为1 m,其质量为1 kg,一质量也为1 kg的小球(视为质点)能在管内运动,管的内径可不计。当小球运动到轨道最高点时,圆轨道对地面的压力刚好为零,取g=10 m/s2。则小球运动到最低点时对轨道的压力大小为
A. 70 NB. 50 NC. 30 ND. 10 N
【答案】A
【解析】
抓住小球运动到最高点时,圆轨道对地面的压力为零,求出最高点的速度,根据动能定理求出小球在最低点的速度,从而结合牛顿第二定律求出轨道对小球的支持力,根据牛顿第三定律得出小球对圆轨道的最大压力.
当小球运动到最高点时速度最小,此时圆轨道对地面的压力为零,可知小球对圆轨道的弹力等于圆轨道的重力,根据牛顿第二定律得,mg+N=m![]() ,N=mg,解得最高点的速度v1=
,N=mg,解得最高点的速度v1= ![]() ;小球从最高点到最低点,根据动能定理得,mg2R=
;小球从最高点到最低点,根据动能定理得,mg2R=![]() ,解得v2=
,解得v2= ![]() ;根据牛顿第二定律得,N′mg=m
;根据牛顿第二定律得,N′mg=m![]() ,联立解得N′=7mg=70N,根据牛顿第三定律,小球对轨道的最大压力N′=7mg=70N,故A正确,BCD错误;
,联立解得N′=7mg=70N,根据牛顿第三定律,小球对轨道的最大压力N′=7mg=70N,故A正确,BCD错误;
故选:A.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目