题目内容
10.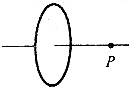 如图所示,一半径为R的圆环,均匀带有电量+q,试计算圆环轴线上与环心相距为x的P点处的场强.
如图所示,一半径为R的圆环,均匀带有电量+q,试计算圆环轴线上与环心相距为x的P点处的场强.
分析 将带电圆环分成若干段,看作若干个点电荷,再根据E=k$\frac{Q}{{r}^{2}}$和矢量的合成,即可求解.
解答 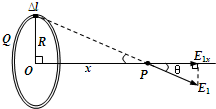 解:将带电圆环分成n段(n→∞),每段都看作点电荷,每个点电荷的电量为q′.
解:将带电圆环分成n段(n→∞),每段都看作点电荷,每个点电荷的电量为q′.
则每个点在P处产生的场强大小为:E1=k$\frac{q′}{{R}^{2}+{x}^{2}}$
根据矢量的合成可得,P处场强大小为:E=nE1cosθ=nk$\frac{q′}{{R}^{2}+{x}^{2}}$•$\frac{x}{\sqrt{{R}^{2}+{x}^{2}}}$=$\frac{kqx}{({R}^{2}+{x}^{2})^{\frac{3}{2}}}$,方向沿x轴正方向.
答:圆环轴线上与环心相距为x的P点处的场强大小为$\frac{kqx}{({R}^{2}+{x}^{2})^{\frac{3}{2}}}$,方向沿x轴正方向.
点评 解决本题的关键是运用微元法,结合数学知识求解合场强.

练习册系列答案
相关题目
1.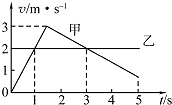 甲、乙两物体沿同一方向做直线运动,t=0时刻经过同一位置,描述两物体运动的v-t图如图,则在0~5s的时间内,关于甲、乙的位置关系下列说法正确的是( )
甲、乙两物体沿同一方向做直线运动,t=0时刻经过同一位置,描述两物体运动的v-t图如图,则在0~5s的时间内,关于甲、乙的位置关系下列说法正确的是( )
 甲、乙两物体沿同一方向做直线运动,t=0时刻经过同一位置,描述两物体运动的v-t图如图,则在0~5s的时间内,关于甲、乙的位置关系下列说法正确的是( )
甲、乙两物体沿同一方向做直线运动,t=0时刻经过同一位置,描述两物体运动的v-t图如图,则在0~5s的时间内,关于甲、乙的位置关系下列说法正确的是( )| A. | 0~1s内,两物体距离越来越小 | B. | 第3s~5s内,两物体距离越来越小 | ||
| C. | 两物体只能相遇一次 | D. | 两物体相遇两次 |
18.关于万有引力定律,正确的是( )
| A. | 万有引力定律是牛顿在总结前人研究的基础上发现的 | |
| B. | 两个物体间的万有引力总是大小相等、方向相反、是一对平衡力 | |
| C. | F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$中的G为引力常量,它是人为规定的 | |
| D. | 测出引力常量的科学家是伽利略 |
5.某人用手将质量为1kg的物体由静止向上提起1m,这时物体的速度为2m/s,取g=10m/s2,则下列说法中正确的是( )
| A. | 物体的动能增加了2J | B. | 物体的重力势能增加了10J | ||
| C. | 物体的动能增加了10J | D. | 手对物体做的功为2J |
15.在电梯内的地板上,竖直放置一根轻质弹簧,弹簧上端固定一个质量为m的物体.当电梯匀速运动时,弹簧被压缩了x,某时刻后观察到弹簧又被继续压缩了$\frac{x}{10}$(重力加速度为g).则电梯在此时刻后的运动情况可能是( )
| A. | 以大小为$\frac{11}{10}$g的加速度加速上升 | B. | 以大小为$\frac{11}{10}$g的加速度减速上升 | ||
| C. | 以大小为$\frac{g}{10}$的加速度加速下降 | D. | 以大小为$\frac{g}{10}$的加速度减速下降 |
2.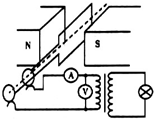 如图所示,为交流发电机、理想变压器和灯光连成的电路,灯光的额定电压为U0,电阻为R.当发电机械圈的转速为n时,灯光正常发光,此时电压表示数为U.图中线圈处于中性面位置,并以此作为计时开始,则有( )
如图所示,为交流发电机、理想变压器和灯光连成的电路,灯光的额定电压为U0,电阻为R.当发电机械圈的转速为n时,灯光正常发光,此时电压表示数为U.图中线圈处于中性面位置,并以此作为计时开始,则有( )
 如图所示,为交流发电机、理想变压器和灯光连成的电路,灯光的额定电压为U0,电阻为R.当发电机械圈的转速为n时,灯光正常发光,此时电压表示数为U.图中线圈处于中性面位置,并以此作为计时开始,则有( )
如图所示,为交流发电机、理想变压器和灯光连成的电路,灯光的额定电压为U0,电阻为R.当发电机械圈的转速为n时,灯光正常发光,此时电压表示数为U.图中线圈处于中性面位置,并以此作为计时开始,则有( )| A. | 变压器输入电压的瞬时值是u=Usin2πnt | |
| B. | 变压器输入电压的瞬时值是u=$\sqrt{2}$Usin2πnt | |
| C. | 电流表的示数是$\frac{U_0^2}{RU}$ | |
| D. | 电流表的示数是$\frac{U}{R}$ |
19. 一定质量的理想气体分别在T1、T2温度下发生等温变化,相应的两条等温线如图所示,T2对应的图线上有A、B两点,表示气体的两个状态.下列叙述正确的是( )
一定质量的理想气体分别在T1、T2温度下发生等温变化,相应的两条等温线如图所示,T2对应的图线上有A、B两点,表示气体的两个状态.下列叙述正确的是( )
 一定质量的理想气体分别在T1、T2温度下发生等温变化,相应的两条等温线如图所示,T2对应的图线上有A、B两点,表示气体的两个状态.下列叙述正确的是( )
一定质量的理想气体分别在T1、T2温度下发生等温变化,相应的两条等温线如图所示,T2对应的图线上有A、B两点,表示气体的两个状态.下列叙述正确的是( )| A. | 温度为T1时气体分子的平均动能比T2时大 | |
| B. | A到B的过程中,气体从外界吸收热量 | |
| C. | A到B的过程中,气体内能增加 | |
| D. | A到B的过程中,气体分子单位时间内对器壁单位面积上的碰撞次数减少 |