题目内容
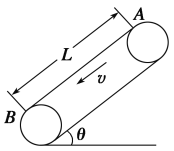
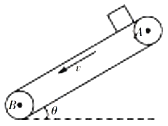
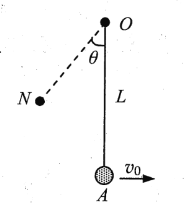
【题目】如图所示,不可伸长的轻质细线下方悬挂一可视为质点的小球,另一端固定在竖直光滑墙面上的O点。开始时,小球静止于A点,现给小球一水平向右的初速度,使其恰好能在竖直平面内绕O点做圆周运动。垂直于墙面的钉子N位于过O点竖直线的左侧,![]() 与
与![]() 的夹角为
的夹角为![]()
![]() ,且细线遇到钉子后,小球绕钉子在竖直平面内做圆周运动,当小球运动到钉子正下方时,细线刚好被拉断。已知小球的质量为m,细线的长度为L,细线能够承受的最大拉力为7mg,g为重力加速度大小。
,且细线遇到钉子后,小球绕钉子在竖直平面内做圆周运动,当小球运动到钉子正下方时,细线刚好被拉断。已知小球的质量为m,细线的长度为L,细线能够承受的最大拉力为7mg,g为重力加速度大小。
(1)求小球初速度的大小![]() ;
;
(2)求小球绕钉子做圆周运动的半径r与![]() 的关系式;
的关系式;
(3)在细线被拉断后,小球继续向前运动,试判断它能否通过A点。若能,请求出细线被拉断时![]() 的值;若不能,请通过计算说明理由。
的值;若不能,请通过计算说明理由。
【答案】(1)![]() (2)
(2)![]() (3)不能通过A点,理由见解析。
(3)不能通过A点,理由见解析。
【解析】
(1) 小球恰能完整圆周运动至最高点,设最高点的速度为v,据圆周运动公式:
![]()
解得:
![]()
小球释放至最高点,由动能定理:
![]()
解得:
![]()
(2)小球绕钉子做圆周运动,设碰到钉子时的速度为![]() ,由释放到碰到钉子时根据动能定理得:
,由释放到碰到钉子时根据动能定理得:
![]()
碰到钉子到绳子断的过程,由动能定理得:
![]()
绳子断的瞬间:
![]()
![]()
联立以上几式,解得:
![]()
(3)细线被拉断后,小球做平抛运动,设t时间小球运动到与A点同一竖直线上,由几何关系德:
![]()
平抛运动水平方向列方程得:
![]()
由(2)可知:
![]()
平抛运动竖直方向列方程得:
![]()
带入上面几式可得:
![]()
平抛开始点与A点的高度差h为:
![]()
若正好过A点,则![]() ,解得:
,解得:
![]()
此结论与(2)不相符,所以小球不能通过A点。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目