题目内容
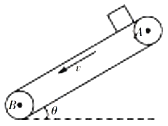
【题目】如图所示，一皮带输送机的皮带以v=10m/s的速率匀速转动，其输送距离AB=29m，与水平方向夹角为θ=37°．将一小物体轻放到A点，物体与皮带间动摩擦因数μ=0.5，已知sin37°=0.6，cos37°=0.8，g=10m/s2，求物体由A到B所需的时间。
【答案】3s
【解析】
设物体运动到C点时速度与传送带相同。物体从A到C的过程，受力如图所示，
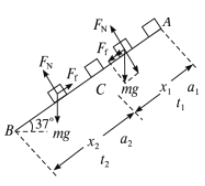
物体开始运动时，受到的滑动摩擦力沿传送带向下，做加速度为a1的匀加速运动，根据牛顿第二定律得
mgsin37°+μmgcos37°=ma1
解得a1=10m/s2
物体速度增大到v=10m/s所用的时间t1=
=
=1s
此过程通过的位移x1=
=
=5m
共速时，因为重力的下滑分力mgsin37°大于最大静摩擦力μmgcos37°，所以物体继续做匀加速运动。
x2=L-x1=24m
根据牛顿第二定律得
mgsin37°-μmgcos37°=ma2
解得a2=2m/s2
由x2=vt2+
at22代入数据解得t2=2s
物体由A到B所需时间为t=t1+t2=3s
练习册系列答案
相关题目
