题目内容
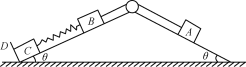
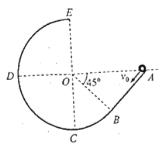
【题目】如图所示,长为![]() m的粗糙直轨道AB与光滑的八分之五的圆轨道BCDE相切于B点且平滑连接。图中的O点为圆轨道的圆心,且E、O、C位于同一条竖直线上(E为圆轨道的最高点);D、O、A于同一条水平线上,且OB与OA的夹角为
m的粗糙直轨道AB与光滑的八分之五的圆轨道BCDE相切于B点且平滑连接。图中的O点为圆轨道的圆心,且E、O、C位于同一条竖直线上(E为圆轨道的最高点);D、O、A于同一条水平线上,且OB与OA的夹角为![]() (OB垂直于AB)。现将一质量
(OB垂直于AB)。现将一质量![]() kg的小球(视为质点)从A点以沿直轨道AB方向的初速度
kg的小球(视为质点)从A点以沿直轨道AB方向的初速度![]() 释放,已知小球与直轨道AB间的动摩擦因数
释放,已知小球与直轨道AB间的动摩擦因数![]() 。
。
(1)若![]() m/s,求小球第一次经过C点时的速度大小;
m/s,求小球第一次经过C点时的速度大小;
(2)若![]() m/s,求整个运动过程中小球对C点压力的最小值;
m/s,求整个运动过程中小球对C点压力的最小值;
(3)若要小球能在运动过程中,既不中途脱离圆轨道,又能再一次回到A点,求![]() 的取值。
的取值。
【答案】(1)![]() ;(2)
;(2)![]() ,方向竖直向下;(3)
,方向竖直向下;(3)![]()
【解析】
(1)小球从A到C过程,据动能定理有
![]()
由几何关系有
![]()
可得
![]()
(2)若恰好到D点,则
![]()
解得
![]()
因为![]() 且
且![]()
可得最终往复运动且![]()
小球从B到C过程,据动能定理
![]()
![]()
得
![]()
根据牛顿第三定律得
![]()
方向竖直向下。
(3)讨论中途不脱离轨道
①若不过D点,则
![]()
解得
![]()
②若能过E点,不中途脱离圆轨道
![]()
从A到E,动能定理
![]()
解得
![]()
讨论能回到A
①沿轨道返回到A点
![]()
得
![]()
舍去(或者其他合理讨论得出不能沿着回到返回A点,只能靠从E点抛出回到A点)
②从E点平抛,到达A点,则
![]()
![]()
联立得
![]()
则
![]()
综上所述只能取![]() 。
。

练习册系列答案
相关题目