Question

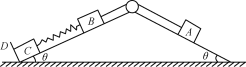
【题目】如图所示，横截面为等腰三角形的光滑斜面，倾角θ=30°，斜面足够长，物块B和C用劲度系数为k的轻弹簧连接，它们的质量均为2m，D为一固定挡板，B与质量为6m的A通过不可伸长的轻绳绕过光滑定滑轮相连接。现固定A，此时绳子伸直无弹力且与斜面平行，系统处于静止状态，然后由静止释放A，则：

(1) 物块C从静止到即将离开D的过程中，重力对B做的功为多少？

(2) 物块C即将离开D时，A的加速度为多少？

(3) 物块C即将离开D时，A的速度为多少？

Answer 1

【答案】(1)； (2)；(3)。

【解析】

(1) 开始系统静止时，对于物块B有

则弹簧压缩量为

C刚离开D时，对于物块C有

则弹簧伸长量为

故A、B的位移大小均为

物块C从静止到刚离开D的过程中，重力对B做功

(2) C刚离开D时，设绳中张力大小为T，对A、B分别由牛顿第二定律有

即

解得A的加速度

(3) 物块C从静止到刚离开D过程中，初末态弹簧的弹性势能相等，

对系统由功能关系得

解得