题目内容
【题目】如图所示,劲度系数为k的轻弹簧一端固定在墙上,另一端与置于水平面上的质量为m的小物体接触(未连接),如图中O点,弹簧水平且无形变.用水平力F缓慢推动物体,在弹性限度内弹簧长度被压缩了x0 , 运动到图中B点,此时物体静止.撤去F后,物体开始向右运动,运动的最大距离B点为3x0 , C点是物体向右运动过程中弹力和摩擦力大小相等的位置,物体与水平面间的动摩擦因数为μ,重力加速度为g.则( )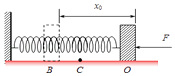
A.撤去F时,弹簧的弹性势能为4μmgx0
B.撤去F后,物体向右运动到C点时的动能最大
C.从B→C物体弹簧弹性势能的减少量等于物体动能的增加量
D.水平力F做的功为4μmgx0
【答案】B,D
【解析】解:A、撤去F后一直到物体停止运动的过程,根据能量守恒得:弹簧的弹性势能 Ep=μmg3x0=3μmgx0,故A错误;
B、撤去F后,物体水平方向上受到弹簧的弹力和滑动摩擦力,滑动摩擦力不变,而弹簧的弹力随着压缩量的减小而减小,弹力先大于摩擦力,合力向右,物体向右加速运动.随着弹力减小,后来弹力小于摩擦力,合力向左,物体向右减速运动,所以当弹力和摩擦力大小相等时,即运动到C点时的动能最大.故B正确;
C、从B→C物体做加速运动,动能增大,由能量守恒可知,弹簧弹性势能的减少量等于物体动能的增加量和产生的内能之和,所以弹簧弹性势能的减少量大于物体动能的增加量,故C错误;
D、物体向左运动过程中,由功能关系知:水平力F做的功为 W=Ep+μmgx0=4μmgx0,故D正确.
故选:BD
研究物体从B向右运动到最右端的过程,由能量守恒求撤去F时弹簧的弹性势能.通过分析物体的受力情况,来确定其运动情况:撤去F后,物体水平方向上受到弹簧的弹力和滑动摩擦力,滑动摩擦力大小不变,而弹簧的弹力随着压缩量的减小而减小,物体先做变加速运动,再做变减速运动,最后物体离开弹簧后做匀减速运动.再结合功能关系分析即可.