题目内容
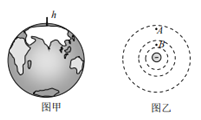
【题目】如图甲所示，一质量为ma的滑块(可看成质点)固定在半径为R的光滑四分之一圆弧轨道的顶端A点，另一质量为mb的滑块(可看成质点)静止在轨道的底端B处，A点和圆弧对应的圆心O点等高。
（1）若圆弧的底端B与水平光滑平面连接(足够长)，mb静止于B点，ma从静止开始释放，假设两滑块碰撞时无机械能损失，且两滑块能发生两次碰撞，试证明：3ma<mb。
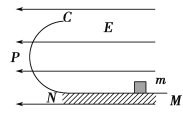
（2）若圆弧的底端B与水平传送带平滑连接，如图乙所示。已知ma=mb=1kg，R=0.8 m，传送带逆时针匀速运行的速率为v0=1 m/s，B点到传送带水平面右端点C的距离为L=2 m。mb静止于B点，ma从静止开始释放，滑块ma与mb相碰后立即结合在一起(设为mc)运动，当mc运动到C点时速度恰好为零。求mc从开始运动到与传送带的速度相同的过程中由于摩擦而产生的热量Q。(g=10 m/s2)
【答案】（1）见解析（2）9J
【解析】
(1)两滑块碰撞时动量守恒mava=mava′＋mbvb′
无机械能损失
ma
=mava′2＋mbvb′2
解得：va′=
解得：vb′=
要想发生两次碰撞必须满足：－va′>vb′代入可得：3ma<mb
(2)机械能守恒magR=
滑块ma与mb相碰后结合在一起，动量守恒mav1=mcv2
从B运动到C点时速度恰好为零，由动能定理可得：
－fL=0－mc
f=mca，－v0=v2－at
mc向右运动：s1=v2t－at2
传送带向左运动：s2=v0t
Q=fs相对=f(s1＋s2)=9J
练习册系列答案
相关题目
