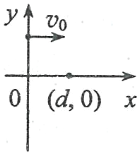题目内容
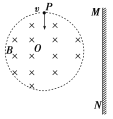
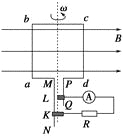
【题目】如图甲所示,一对平行金属板M、N长为L,相距为d,O1O为中轴线.其中N板接地.当M板的电势φ=φ0时,两板间为匀强电场,忽略两极板外的电场某种电荷量为q的带负电的粒子从O1点以速度v0沿O1O方向射入电场,粒子恰好打在上极板M的中点,粒子重力忽略不计

(1)求粒子的质量;
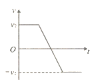
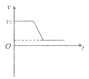
(2)若M板的电势变化如图乙所示,其周期T=![]() ,从t=0开始,前
,从t=0开始,前![]() 内φM=2φ,后
内φM=2φ,后![]() 内φM=—φ,大量的上述粒子仍然以速度v0沿O1O方向持续射入电场,最终所有粒子恰好能全部离开电场而不打在极板上,求φ的值;
内φM=—φ,大量的上述粒子仍然以速度v0沿O1O方向持续射入电场,最终所有粒子恰好能全部离开电场而不打在极板上,求φ的值;
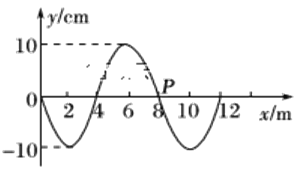
(3)紧贴板右侧建立直角坐标系xOy,在xOy坐标平面的第IIV象限内存在一个圆形的匀强磁场区域,磁场方向垂直于该坐标平面,要使在(2)问情景下所有粒子经过磁场偏转后都会聚于P(1.5d,1.5d)点,求磁感应强度B的大小范围
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
![]()
【解析】
(1)设粒子经过时间![]() 打在M板中点,
打在M板中点,
沿极板方向:![]() ,
,
垂直极板方向:![]() ,整理得到:
,整理得到:![]()
(2)粒子通过两板时间![]()
从![]() 时刻开始,粒子在两板间运动时每个电势变化周期的前三分之一时间内的加速度大小为
时刻开始,粒子在两板间运动时每个电势变化周期的前三分之一时间内的加速度大小为![]() ,方向垂直极板向上;在每个电势变化周期的后三分之二时间内加速度大小为
,方向垂直极板向上;在每个电势变化周期的后三分之二时间内加速度大小为![]() ,方向垂直极板向下,不同时刻从
,方向垂直极板向下,不同时刻从![]() 点进入电场的粒子在电场方向的速度
点进入电场的粒子在电场方向的速度![]() 随时间
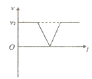
随时间![]() 变化的关系如图1所示:
变化的关系如图1所示:
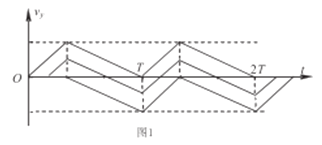
因为所有粒子刚好能全部离开电场而不打在极板上,可以确定在![]() 或
或![]() 时刻进入电场的粒子恰好分别从极板右侧上下边缘处飞出,它们在电场方向偏转的距离最大,
时刻进入电场的粒子恰好分别从极板右侧上下边缘处飞出,它们在电场方向偏转的距离最大,![]() ,整理可以得到:
,整理可以得到:![]() .
.
(3)所有粒子射出电场时速度方向都平行于![]() 轴,大小为
轴,大小为![]() ,设粒子在磁场中运动半径为
,设粒子在磁场中运动半径为![]() ,则
,则![]() ,整理可得到:
,整理可得到:![]() .粒子进入圆形区域内聚焦于P点
.粒子进入圆形区域内聚焦于P点![]() 时,磁场区半径R应满足:
时,磁场区半径R应满足:![]() ,在圆形磁场区域边界上,P点纵坐标有最大值,如图2所示:
,在圆形磁场区域边界上,P点纵坐标有最大值,如图2所示:

磁场区的最小半径![]() ,对应磁感应强度有最大值
,对应磁感应强度有最大值![]()
磁场区的最大半径![]() ,对于磁感应强度有最小值为
,对于磁感应强度有最小值为![]()
所以,磁感应强度B的大小可能范围![]()
![]() .
.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案