Question

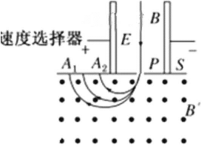
【题目】如图，空间区域Ⅰ、Ⅱ有匀强电场和匀强磁场，MN、PQ为理想边界，Ⅰ区域高度为d，Ⅱ区域的高度足够大匀强电场方向竖直向上；Ⅰ、Ⅱ区域的磁感应强度大小均为B，方向分别垂直纸面向里和向外一个质量为m，电量为q的带电小球从磁场上方的O点由静止开始下落，进入场区后，恰能做匀速圆周运动已知重力加速度为g．

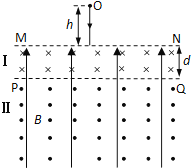
（1）试判断小球的电性并求出电场强度E的大小；

（2）若带电小球能进入区域Ⅱ，则h应满足什么条件？

（3）若带电小球运动一定时间后恰能回到O点，求它释放时距MN的高度h．

Answer 1

【答案】正电，；；．

【解析】

(1)根据小球所受电场力的方向与场强方向的关系判断小球电性，根据电场力与重力的关系求出电场强度大小．

(2)由机械能守恒定律求出小球进入磁场时的速度，小球在磁场中做匀速圆周运动，作出小球的运动轨迹，由几何知识求出轨道半径，应用牛顿第二定律分析答题．

(3)由机械能守恒定律、牛顿第二定律与几何知识求出h．

（1）带电小球进入复合场后，恰能做匀速圆周运动，合力为洛伦兹力，重力与电场力平衡，重力竖直向下，电场力竖直向上，即小球带正电
由
解得：
（2）假设下落高度为时，带电小球在Ⅰ区域作圆周运动的圆弧与PQ相切时，运动轨迹如答图所示

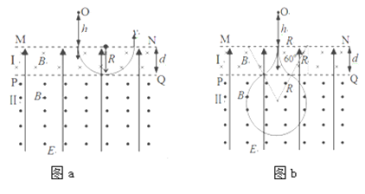
由几何知识可知，小球的轨道半径：
带电小球在进入磁场前做自由落体运动，由机械能守恒定律得：
带电小球在磁场中作匀速圆周运动，设半径为R，由牛顿第二定律得：
解得：，
则当时，即带电小球能进入Ⅱ区域；
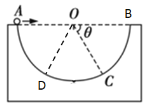
（3）由于带电小球在Ⅰ、Ⅱ两个区域运动过程中q、v、B、m的大小不变，故三段圆周运动的半径相同，以三个圆心为顶点的三角形为等边三角形，边长为2R，内角为，如答图所示由几何关系知：
联立解得得：；