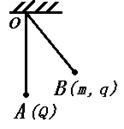题目内容
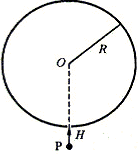
（25分）图示为一固定不动的绝缘的圆筒形容器的横截面，其半径为 R，圆筒的轴线在 O 处。圆筒内有匀强磁场，磁场方向与圆筒的轴线平行，磁感应强度为 B 。筒壁的 H 处开有小孔，整个装置处在真空中。现有一质量为 m、电荷量为 q 的带电粒子 P 以某一初速度沿筒的半径方向从小孔射入圆筒，经与筒壁碰撞后又从小孔射出圆筒。设：筒壁是光滑的，P 与筒壁碰撞是弹性的，P 与筒壁碰撞时其电荷量是不变的。若要使 P 与筒壁碰撞的次数最少，问：
1. P 的速率应为多少？
2. P从进入圆筒到射出圆筒经历的时间为多少？
参考答案：
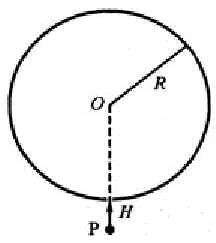
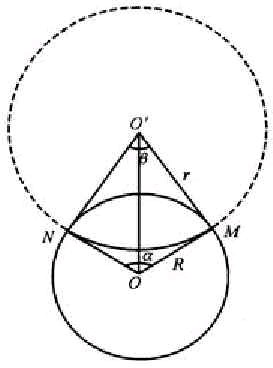
1. 如图1所示，设筒内磁场的方向垂直纸面指向纸外，带电粒子 P 带正电，其速率为 v 。P 从小孔射入圆筒中，因受到磁场的作用力而偏离入射方向，若与筒壁只发生一次碰撞，是不可能从小孔射出圆筒的。但与筒壁碰撞两次，它就有可能从小孔射出。造此情形中，P 在筒内的路径由三段等长、等半径的圆弧 HM、MN、和 NH 组成。现考察其中一段圆弧 MN，如图2所示。由于 P 沿筒的半径方向入射，OM 和 ON 均与轨道相切，两者的夹角
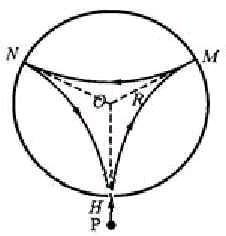
（1）
设圆弧的圆半径为 r ，则有
（2）
圆弧对轨道圆心 
所张的圆心角
（3）
由几何关系得
（4）
解（2）、（3）、（4）式得
（5）
2. P 由小孔射入到第一次与筒壁碰撞所通过的路径为
（6）
经历时间为
（7）
P 从射入小孔到射出小孔经历的时间为
（8）
由以上有关各式得
（9）
