Question

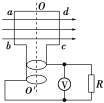
【题目】早期一种氢原子模型（汤姆生模型），它是均匀带正电的球，电子位于球心，整个原子呈中性，试求这样原子的半径．如果已知，为使电子脱离离子飞向远处，它需要具有的最小能量等于，电子电量为e．

Answer 1

【答案】

【解析】

首先不难计算将电子从原子表面移到无穷远处需要做的功，这功等于电子在带正电球面处具有的电势能，即电场在球面上的电势（e是球的电量，R是球的半径）乘以电子的电量

为了求得电子从原子中心移到其表面需要做的功，将球分成许多厚为的薄球层，使在每一层范围内作用在电荷上的力可以认为是恒定的，为此必须使．每层电荷产生的电场强度在内层等于零，而在层外，如同整层电荷集中在球心所产生的电场强度．在原子内到球心距离r处电场强度等于

在这层对电子作用力为．

式中q是半径为r球内电量。

因为球的电量为e且在球体内均匀分布，所以在球的单位体积内聚集电量为．

这就是说，在半径为r球内将有电量

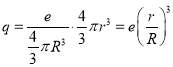
所以．

为了求在原子内部移动电子做的功，取平均力并乘以电子位移R．因为作用在电子上的力与电子到原子中心距离成正比，所以平均力等于电子在原子表面上所受力的一半：，

所以

将电子从原子中心移到远处需要做的总功为

据题意这个功等于，即，

由此得．