��Ŀ����
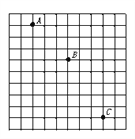
����Ŀ�����Ż���Ӱ������� P1��P2������һ�Ž������� S1��S2 ����������Բ���˶���ͼ�������ʾ������Χ�ռ�ijλ�õ��������ٶ�a�������ʾijλ�õ��������ľ��� r ƽ���ĵ�����a��![]() ��ϵ��ͼ��ʾ������ S1��S2 ���������ٶȴ�С��Ϊ a0������ ��
��ϵ��ͼ��ʾ������ S1��S2 ���������ٶȴ�С��Ϊ a0������ ��

A. S1�������� S2 ��С
B. P1 �������� P2 ��С
C. P1�ĵ�һ�����ٶȱ�P2 �Ĵ�
D. P1 ��ƽ���ܶȱ� P2 ��С
���𰸡�CD
��������A��B������ţ�ٵڶ����ɵã�![]() ��������Ƕ���Χ�ռ������������������ļ��ٶ�Ϊ��
��������Ƕ���Χ�ռ������������������ļ��ٶ�Ϊ��![]() ���ɴ˲����жϽ�������S1��S2��������С������ѧ֪ʶ֪��
���ɴ˲����жϽ�������S1��S2��������С������ѧ֪ʶ֪��![]() ͼ���б�ʵ���GM��б��Խ��GMԽ��MԽ������P1��������P2�Ĵ�A��B����C�����һ�����ٶ�Ϊv����
ͼ���б�ʵ���GM��б��Խ��GMԽ��MԽ������P1��������P2�Ĵ�A��B����C�����һ�����ٶ�Ϊv����![]() ����
����![]() ����ͼ������P1�İ뾶��P2�İ뾶��a0��ȣ���֪P1�ĵ�һ�����ٶȱ�P2�Ĵ�C��ȷ��D�����ǵ�ƽ���ܶ�
����ͼ������P1�İ뾶��P2�İ뾶��a0��ȣ���֪P1�ĵ�һ�����ٶȱ�P2�Ĵ�C��ȷ��D�����ǵ�ƽ���ܶ� ��P1�İ뾶��P2�İ뾶��a0��ȣ���P1��ƽ���ܶȱ�P2��С����D��ȷ����ѡCD��
��P1�İ뾶��P2�İ뾶��a0��ȣ���P1��ƽ���ܶȱ�P2��С����D��ȷ����ѡCD��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ