题目内容
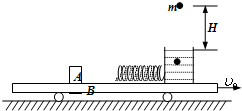 如图所示,光滑水平面上有一小车B,右端固定一砂箱,砂箱左侧连接一水平轻弹簧,小车和砂箱的总质量为M.车上放有一小物块A,质量也为M.物块A随小车以速度υ0向右匀速运动.物块A与其左侧的车面的动摩擦因数为μ,与其它车面的摩擦不计.在车匀速运动的过程中,距砂面H高处有一质量为m=
如图所示,光滑水平面上有一小车B,右端固定一砂箱,砂箱左侧连接一水平轻弹簧,小车和砂箱的总质量为M.车上放有一小物块A,质量也为M.物块A随小车以速度υ0向右匀速运动.物块A与其左侧的车面的动摩擦因数为μ,与其它车面的摩擦不计.在车匀速运动的过程中,距砂面H高处有一质量为m=| M |
| 2 |
| H |
| 5 |
(1)小车在前进中,弹簧弹性势能的最大值是多少?
(2)为使物块A不从小车上滑下,车面粗糙部分至少多长?
(3)从泥球下落至物块相对小车静止的全过程中,A、B、C系统产生总内能为多少?
分析:1、泥球落入砂箱时,水平方向动量守恒.由于泥球水平方向的速度为0,故碰撞后小车的速度减小.而A的速度不变(A右侧无摩擦),因此,A将与弹簧碰撞,压缩弹簧.在弹簧弹力作用下,A减速,小车加速.只要A的速度大于小车的速度,A将继续压缩弹簧,弹簧的弹性势能将继续增大.当A的速度等于小车速度时,弹簧压缩到最短,此时其弹性势能最大.此后,A继续减速,小车继续加速,A的速度小于小车的速度,弹簧的压缩量减小,弹性势能变小.
2、由1可知,当弹簧恢复原长时,A必相对于小车向左滑动.当A滑上粗糙部分后,在摩擦力作用下,最后相对于小车静止.从A滑上小车粗糙部分开始到相对小车静止的过程中,A相对于小车滑行的距离即为所要求的最小距离.
3、根据能量守恒列出等式求解.
2、由1可知,当弹簧恢复原长时,A必相对于小车向左滑动.当A滑上粗糙部分后,在摩擦力作用下,最后相对于小车静止.从A滑上小车粗糙部分开始到相对小车静止的过程中,A相对于小车滑行的距离即为所要求的最小距离.
3、根据能量守恒列出等式求解.
解答:解:(1)依题意,当A与小车的速度再次相等时,弹簧的弹性势能最大.
泥球落入砂箱过程中,车与泥球系统水平方向动量守恒.
设泥球落入砂箱后车速为v1.有:
Mv0=(M+m)v1
从A开始压缩弹簧到两者速度相等的过程中,系统动量守恒.
设系统的共同速度为v2,有:
Mv0+(M+m)v1=(M+M+m)v2
Ep=
M
+
(M+m)
-
(2M+m)
从A开始压缩弹簧到两者速度相等的过程中,系统损失的动能转化为弹簧的弹性势能.有:
Ep=
(2)从弹簧压缩最短到A受摩擦力作用而再次相对小车静止的过程中,系统动量守恒.
因此,A相对小车静止后,它们的共同速度必等于v2,即此过程始、末状态系统的动能未变,
因此,弹簧减少的弹性势能通过摩擦力做功转化为系统的内能.
设A相对于小车滑行的距离为L.有:μMgL=EP
L=
(3)根据能量守恒得:△E=mg(H+h)+
?2M?
-
(2M+m)
即系统产生的总内能为:△E=
M(3gH+
)
答:(1)小车在前进中,弹簧弹性势能的最大值是Ep=
(2)为使物块A不从小车上滑下,车面粗糙部分至少
(3)从泥球下落至物块相对小车静止的全过程中,A、B、C系统产生总内能为△E=
M(3gH+
)
泥球落入砂箱过程中,车与泥球系统水平方向动量守恒.
设泥球落入砂箱后车速为v1.有:
Mv0=(M+m)v1
从A开始压缩弹簧到两者速度相等的过程中,系统动量守恒.
设系统的共同速度为v2,有:
Mv0+(M+m)v1=(M+M+m)v2
Ep=
| 1 |
| 2 |
| V | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
从A开始压缩弹簧到两者速度相等的过程中,系统损失的动能转化为弹簧的弹性势能.有:
Ep=
| ||
| 2(M+m)(2M+m) |
(2)从弹簧压缩最短到A受摩擦力作用而再次相对小车静止的过程中,系统动量守恒.
因此,A相对小车静止后,它们的共同速度必等于v2,即此过程始、末状态系统的动能未变,
因此,弹簧减少的弹性势能通过摩擦力做功转化为系统的内能.
设A相对于小车滑行的距离为L.有:μMgL=EP
L=
| ||
| 2μg(M+m)(2M+m) |
(3)根据能量守恒得:△E=mg(H+h)+
| 1 |
| 2 |
| υ | 2 0 |
| 1 |
| 2 |
| υ | 2 2 |
即系统产生的总内能为:△E=
| 1 |
| 5 |
| υ | 2 0 |
答:(1)小车在前进中,弹簧弹性势能的最大值是Ep=
| ||
| 2(M+m)(2M+m) |
(2)为使物块A不从小车上滑下,车面粗糙部分至少
| ||
| 2μg(M+m)(2M+m) |
(3)从泥球下落至物块相对小车静止的全过程中,A、B、C系统产生总内能为△E=
| 1 |
| 5 |
| υ | 2 0 |
点评:解决该题关键要掌握动量守恒和能量守恒列出等式求解,注意小球掉小车的过程中是小球与车水平方向的动量守恒.

练习册系列答案
相关题目
 如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相接,导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动完成半个圆周运动恰好到达C点.试求:
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相接,导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动完成半个圆周运动恰好到达C点.试求: 如图所示,光滑水平面与一半径为R处在竖平面内的光滑圆轨道相切,质量为m的小球(可视为质点)以初速度v0向右运动进入圆轨道,在图中虚线位置脱离轨道,重力加速度为g,下述说法正确的是( )
如图所示,光滑水平面与一半径为R处在竖平面内的光滑圆轨道相切,质量为m的小球(可视为质点)以初速度v0向右运动进入圆轨道,在图中虚线位置脱离轨道,重力加速度为g,下述说法正确的是( )
 (2013?如东县模拟)如图所示,光滑水平面AB与竖直面内粗糙的半圆形导轨在B点衔接,BC为导轨的直径,与水平面垂直,导轨半径为R,一个质量为m的小球将弹簧压缩至A处.小球从A处由静止释放被弹开后,以速度v经过B点进入半圆形轨道,之后向上运动恰能沿轨道运动到C点,求:
(2013?如东县模拟)如图所示,光滑水平面AB与竖直面内粗糙的半圆形导轨在B点衔接,BC为导轨的直径,与水平面垂直,导轨半径为R,一个质量为m的小球将弹簧压缩至A处.小球从A处由静止释放被弹开后,以速度v经过B点进入半圆形轨道,之后向上运动恰能沿轨道运动到C点,求: 如图所示,光滑水平面内,一根细绳一端固定,另一端系一小球,现让小球在水平面内做匀速圆周运动,则( )
如图所示,光滑水平面内,一根细绳一端固定,另一端系一小球,现让小球在水平面内做匀速圆周运动,则( )