题目内容
2.以水平地面为零势面,将小球从水平地面竖直向上抛出,A为小球运动过程中的某一点,在上升过程中,小球经过该点时的动能是其势能的两倍,在下落过程中,小球经过该点时的势能是动能的两倍,已知小球能够达到的最大高度为H,且小球在运动过程中所受空气阻力大小恒定,求A点距水平地面的高度h.分析 对小球从地面到最高点过程、从地面到A点过程、从最高点下落到A点过程,分别运用动能定理列式,结合动能和势能的关系列式,联立可解
解答 解:设空气阻力大小为f.对小球根据动能定理得:
从地面到最高点过程有:-mgH-fH=0-$\frac{1}{2}$…①
从地面到A点过程有:-mgh-fh=$\frac{1}{2}$-$\frac{1}{2}$…②
从最高点下落到A点过程有:(mg-f)(H-h)=$\frac{1}{2}$…③
据题有:2mgh=$\frac{1}{2}$…④
mgh=2×$\frac{1}{2}$…⑤
联立①②④解得:f=$\frac{3h-H}{H-h}$…⑥
联立③⑤⑥解得:h=$\frac{4}{9}$H
答:A点距水平地面的高度h为$\frac{4}{9}$H
点评 本题是多过程问题,运用动能定理时,要灵活选择研究的过程,同时要把握已知条件,得到动能与势能的关系

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
12.以下对物理学发展史的说法正确的是( )
| A. | 库仑利用扭秤实验测得了引力常数 | |
| B. | 法拉第为了形象地描述电场首次引入电场线的概念 | |
| C. | 牛顿在前人积累的数据上提出了万有引力定律 | |
| D. | 开普勒利用理想斜面实验推翻了亚里士多德关于运动需要力来维持的观点 |
13.关于粒子的说法,正确的是( )
| A. | 组成阴极射线的带电粒子是α粒子 | |
| B. | 卢瑟福在利用α粒子轰击氮原子核的实验中发现了质子 | |
| C. | 发生光电效应时,从金属表面逸出的粒子是光子 | |
| D. | 查德威克在利用α粒子轰击铍原子核的实验中发现了电子 |
7.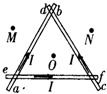 如图所示,三根彼此绝缘的无限长直导线的一部分ab、cd、ef构成一个等边三角形,O为三角形的中心,M、N分别为O关于导线ab、cd的对称点,当三根导线中通以大小相等,方向如图所示的电流时,M点磁感应强度的大小为B1,O点磁感应强度的大小为B2,若将导线ab中的电流撤去,而保持另两根导线中的电流不变,则N点磁感应强度的大小为( )
如图所示,三根彼此绝缘的无限长直导线的一部分ab、cd、ef构成一个等边三角形,O为三角形的中心,M、N分别为O关于导线ab、cd的对称点,当三根导线中通以大小相等,方向如图所示的电流时,M点磁感应强度的大小为B1,O点磁感应强度的大小为B2,若将导线ab中的电流撤去,而保持另两根导线中的电流不变,则N点磁感应强度的大小为( )
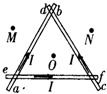 如图所示,三根彼此绝缘的无限长直导线的一部分ab、cd、ef构成一个等边三角形,O为三角形的中心,M、N分别为O关于导线ab、cd的对称点,当三根导线中通以大小相等,方向如图所示的电流时,M点磁感应强度的大小为B1,O点磁感应强度的大小为B2,若将导线ab中的电流撤去,而保持另两根导线中的电流不变,则N点磁感应强度的大小为( )
如图所示,三根彼此绝缘的无限长直导线的一部分ab、cd、ef构成一个等边三角形,O为三角形的中心,M、N分别为O关于导线ab、cd的对称点,当三根导线中通以大小相等,方向如图所示的电流时,M点磁感应强度的大小为B1,O点磁感应强度的大小为B2,若将导线ab中的电流撤去,而保持另两根导线中的电流不变,则N点磁感应强度的大小为( )| A. | B1+B2 | B. | B1-B2 | C. | $\frac{1}{2}$(B1+B2) | D. | $\frac{1}{2}$(3B2-B1) |
14.如果取弹簧伸长△x时的弹性势能为0,则下列说法中正确的是( )
| A. | 弹簧处于原长时,弹簧的弹性势能为正值 | |
| B. | 弹簧处于原长时,弹簧的弹性势能为负值 | |
| C. | 当弹簧的压缩量为△x时,弹性势能的值为0 | |
| D. | 只要弹簧被压缩,弹性势能的值都为负值 |
11. 如图所示,一束单色光从空气入射到棱镜的AB面上,经AB和AC两个面折射后从AC面进入空气,当出射角i′和入射角i相等时,出射光线相对于入射光线偏转的角度为θ,已知棱镜顶角为α,则计算棱镜对该色光的折射率表达式为( )
如图所示,一束单色光从空气入射到棱镜的AB面上,经AB和AC两个面折射后从AC面进入空气,当出射角i′和入射角i相等时,出射光线相对于入射光线偏转的角度为θ,已知棱镜顶角为α,则计算棱镜对该色光的折射率表达式为( )
 如图所示,一束单色光从空气入射到棱镜的AB面上,经AB和AC两个面折射后从AC面进入空气,当出射角i′和入射角i相等时,出射光线相对于入射光线偏转的角度为θ,已知棱镜顶角为α,则计算棱镜对该色光的折射率表达式为( )
如图所示,一束单色光从空气入射到棱镜的AB面上,经AB和AC两个面折射后从AC面进入空气,当出射角i′和入射角i相等时,出射光线相对于入射光线偏转的角度为θ,已知棱镜顶角为α,则计算棱镜对该色光的折射率表达式为( )| A. | $\frac{sin\frac{α+θ}{2}}{sin\frac{α}{2}}$ | B. | $\frac{sin\frac{α+θ}{2}}{sin\frac{θ}{2}}$ | C. | $\frac{sinθ}{sin(θ-\frac{α}{2})}$ | D. | $\frac{sinα}{sin(α-\frac{θ}{2})}$ |
12.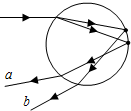 中国古人对许多自然现象有深刻认识,唐人张志和在《玄真子•涛之灵》中写道:“雨色映日而为虹”.从物理学角度看,虹是太阳光经过雨滴的两次折射和一次反射形成的.如图是彩虹成因的简化示意图,其中a、b是两种不同频率的单色光,则两光( )
中国古人对许多自然现象有深刻认识,唐人张志和在《玄真子•涛之灵》中写道:“雨色映日而为虹”.从物理学角度看,虹是太阳光经过雨滴的两次折射和一次反射形成的.如图是彩虹成因的简化示意图,其中a、b是两种不同频率的单色光,则两光( )
 中国古人对许多自然现象有深刻认识,唐人张志和在《玄真子•涛之灵》中写道:“雨色映日而为虹”.从物理学角度看,虹是太阳光经过雨滴的两次折射和一次反射形成的.如图是彩虹成因的简化示意图,其中a、b是两种不同频率的单色光,则两光( )
中国古人对许多自然现象有深刻认识,唐人张志和在《玄真子•涛之灵》中写道:“雨色映日而为虹”.从物理学角度看,虹是太阳光经过雨滴的两次折射和一次反射形成的.如图是彩虹成因的简化示意图,其中a、b是两种不同频率的单色光,则两光( )| A. | 在同种玻璃中传播,a光的传播速度一定大于b光 | |
| B. | 以相同角度斜射到同一玻璃板透过平行表面后,b光侧移量大 | |
| C. | 分别照射同一光电管,若b光能引起光电效应,a光也一定能 | |
| D. | 以相同的入射角从水中射入空气,在空气中只能看到一种光时,一定是a光 |
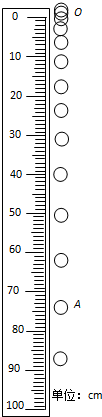 为验证小球在自由下落过程中机械能守恒,某实验小组进行了如下操作:
为验证小球在自由下落过程中机械能守恒,某实验小组进行了如下操作: