题目内容
如图所示,在场强大小为E的匀强电场中,一根不可伸长的绝缘细线一端栓一个质量为m,电荷量为q的带负电的小球,另一端固定在O点,把小球拉到使细线水平的位置A,然后将小球由静止释放,小球沿弧线运动到细线与水平方向成θ=60°的位置B时速度为零,以下说法正确的是( )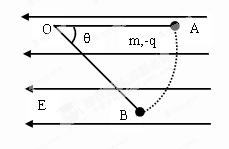
A.小球重力与电场力的大小关系是qE=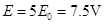 mg mg |
B.小球重力与电场力的大小关系是mg=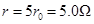 qE qE |
| C.小球在B点时,细线拉力T=2qE |
D.小球在B点时,细线拉力T=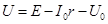 mg mg |
AD
解析试题分析:从A到B的过程中,根据动能定理,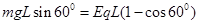 ,可得,qE=
,可得,qE=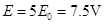 mg,A正确,B错误;到达B点时,速度为零,将所有的力沿着半径和垂直于半径分解,在沿着半径方向合力为零,可知,
mg,A正确,B错误;到达B点时,速度为零,将所有的力沿着半径和垂直于半径分解,在沿着半径方向合力为零,可知, ,因此D正确,C错误。
,因此D正确,C错误。
考点:动能定理,物体受力分析

 名校课堂系列答案
名校课堂系列答案现将一边长为l、在如图所示的两平行虚线之间存在着垂直纸面向里、宽度为d、磁感应强度为B的匀强磁场,正方形线框abcd的边长为L(L<d)、质量为m、电阻为R。将线框从距离磁场的上边界为h高处由静止释放后,线框的ab边刚进入磁场时的速度为 ,ab边刚离开磁场时的速度也为,在线框开始进入到全部离开磁场的过程中( )
,ab边刚离开磁场时的速度也为,在线框开始进入到全部离开磁场的过程中( )
| A.线圈ab边进场阶段一定减速 |
| B.线圈ab边进场阶段可能匀速 |
| C.感应电流所做的功为mgd |
| D.感应电流所做的功为2mgd |
如图所示,在绝缘的斜面上方存在着沿水平向右的匀强电场,斜面上的带电金属块沿斜面滑下。已知在下滑的过程中,金属块动能增加了12J,金属块克服摩擦力做功8J,重力做功24J,下列判断中正确的是( )
| A.金属块带负电 |
| B.金属块克服电场力做功8J |
| C.金属块的机械能减少12J |
| D.金属块的电势能减少4J |
一个带正电荷q、质量为m的小球,从光滑绝缘的斜面轨道的A点由静止下滑,小球恰能通过半径为R的光滑绝缘竖直圆形轨道的最高点B而做圆周运动。现在竖直方向上加如图所示的匀强电场,若仍从A点由静止释放该小球,则( ) 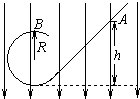
| A.小球不能过B点 |
| B.小球仍然恰好能过B点 |
| C.小球能过B点,且在B点与轨道之间压力不为0 |
| D.以上说法都不对 |
一个初动能为Ek的带电粒子,以速度v沿垂直电场线方向飞入两块平行金属板间(带等量异号电荷且正对放置),飞出时动能为3Ek.如果这个带电粒子的初速度增加到原来的2倍,仍从原位置沿原方向射入,不计重力,那么该粒子飞出时动能为 ( )
| A.4.5Ek | B.4Ek | C.6Ek | D.9.5Ek |
如图所示,在点电荷Q的电场中,已知a、b两点在同一等势势面上,c、d两点在同一等势面上,无穷远处电势为零.甲、乙两个带电粒子经过a点时动能相同,甲粒子的运动轨迹为acb,乙粒子的运动轨迹为adb.由此可以判定( )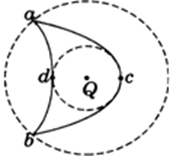
| A.甲粒子经过c点与乙粒子经过d点时的动能相等 |
| B.甲、乙两粒子带异种电荷 |
| C.甲粒子经过c点时的电势能小于乙粒子经过d点时的电势能 |
| D.两粒子经过b点时具有相同的动能 |



