题目内容
(12分)如图所示,一质量不计的轻质弹簧的上端与盒子A连接在一起,盒子A放在倾角为θ=300的光滑固定斜面上,下端固定在斜面上.盒子内装一个光滑小球,盒子内腔为正方体,一直径略小于此正方形边长的金属圆球B恰好能放在盒内,已知弹簧劲度系数为k=100N/m,盒子A和金属圆球B质量均为1kg.,将A沿斜面向上提起,使弹簧从自然长度伸长10cm,从静止释放盒子A,A和B一起在斜面上做简谐振动,g取10m/s2,求:
(1)盒子A的振幅.
(2)金属圆球B的最大速度. (弹簧型变量相同时弹性势能相等)
(3)盒子运动到最高点时,盒子A对金属圆球B的作用力大小
(1) 20cm(2)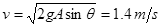 (3)5N
(3)5N
解析试题分析:(1) 振子在平衡位置时,所受合力为零,设此时弹簧被压缩Δx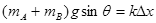 (1分)
(1分)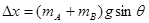 /
/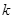 =10cm(1分)
=10cm(1分)
释放时振子处在最大位移处,故振幅A为: A=10cm+10cm=20cm(2分)
(2)由于开始时弹簧的伸长量恰等于振子在平衡位置时弹簧的压缩量,故弹簧势能相等,设振子的最大速率为v,从开始到平衡位置,根据机械能守恒定律: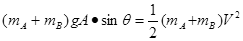 (2分)
(2分)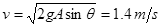 (2分)
(2分)
(3)在最高点振子受到的重力分力和弹力方向相同,根据牛顿第二定律: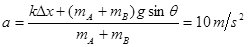 (2分)(或由对称性可得)
(2分)(或由对称性可得)
A对B的作用力方向向下,其大小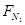 为:
为: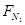 =
=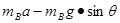 =5N (2分)
=5N (2分)
考点:简谐运动、机械能守恒定律、牛顿第二定律

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
在探究物体的加速度a与物体所受外力F、物体质量M间的关系时,采用如图所示的实验装置.小车及车中的砝码质量用M表示,盘及盘中的砝码质量用m表示.
(1)当M与m的大小关系满足________时,才可以认为绳子对小车的拉力大小等于盘和砝码的重力.
(2)某一组同学先保持盘及盘中的砝码质量m一定来做实验,其具体操作步骤如下,以下做法正确的是________.
| A.平衡摩擦力时,应将盘及盘中的砝码用细绳通过定滑轮系在小车上 |
| B.每次改变小车的质量时,不需要重新平衡摩擦力 |
| C.实验时,先放开小车,再接通打点计时器的电源 |
D.用天平测出m以及小车质量M,小车运动的加速度可直接用公式a= 求出 求出 |

图1 图2
图1: ____________________________________________________;
图2: _____________________________________________________.
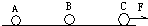
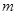 的光滑1/4圆形轨道,BC段为高为h=5
的光滑1/4圆形轨道,BC段为高为h=5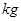 的小球由A点从静止开始下滑到B点时速度的大小为2
的小球由A点从静止开始下滑到B点时速度的大小为2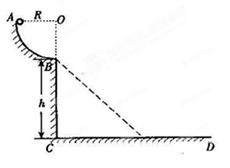
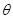 =45°的斜面(如图中虚线所示),那么小球离开B点后能否落到斜面上?如果能,求它第一次落在斜面上的位置。
=45°的斜面(如图中虚线所示),那么小球离开B点后能否落到斜面上?如果能,求它第一次落在斜面上的位置。 。汽车在足够长的水平路面从静止以0.6m/s2的加速度做匀加速直线运动。(已知汽车在行驶中所受路面阻力恒定为重力的0.1倍,g取10m/s2)求:
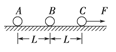
。汽车在足够长的水平路面从静止以0.6m/s2的加速度做匀加速直线运动。(已知汽车在行驶中所受路面阻力恒定为重力的0.1倍,g取10m/s2)求:  圆弧光滑轨道,底端与传送带相切。传送带长也为R。传送带右端接光滑的水平面,水平面上静止放置一质量为3m的小物块B。一质量为m的小物块A从圆弧轨道顶端由静止释放,经过传送带后与B发生碰撞,碰后A以碰前速率的一半反弹。A与B碰撞后马上撤去圆弧轨道。已知物块A与传送带的动摩擦因数为μ=0.5,取重力加速度为g,传送带逆时针运动的速度的取值范围为
圆弧光滑轨道,底端与传送带相切。传送带长也为R。传送带右端接光滑的水平面,水平面上静止放置一质量为3m的小物块B。一质量为m的小物块A从圆弧轨道顶端由静止释放,经过传送带后与B发生碰撞,碰后A以碰前速率的一半反弹。A与B碰撞后马上撤去圆弧轨道。已知物块A与传送带的动摩擦因数为μ=0.5,取重力加速度为g,传送带逆时针运动的速度的取值范围为 .求:
.求:
 竖直放置的光滑细圆管,O为细圆管的圆心,在圆管的末端C连接倾斜角为450、
竖直放置的光滑细圆管,O为细圆管的圆心,在圆管的末端C连接倾斜角为450、 的足够长粗糙斜面,一质量为m=0.5kg的小球从O点正上方某处A点以V0水平抛出,恰好能垂直OB从B点进入细圆管,小球从进入圆管开始受到始终竖直向上的力F=5N的作用,当小球运动到圆管的末端C时作用力F立即消失,能平滑的冲上粗糙斜面。(g=10m/s2)求:
的足够长粗糙斜面,一质量为m=0.5kg的小球从O点正上方某处A点以V0水平抛出,恰好能垂直OB从B点进入细圆管,小球从进入圆管开始受到始终竖直向上的力F=5N的作用,当小球运动到圆管的末端C时作用力F立即消失,能平滑的冲上粗糙斜面。(g=10m/s2)求:
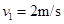 ,乙小球冲上速度为
,乙小球冲上速度为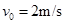 的水平传送带上(传送带速度保持不变),乙与传送带之间的动摩擦因数
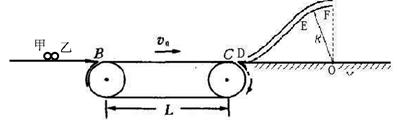
的水平传送带上(传送带速度保持不变),乙与传送带之间的动摩擦因数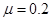 ,DEF是光滑细圆管,其中D点与水平面相切,EF是半经为R=0.1m圆弧,乙小球的直经比细管直经略小点,乙小球离开传送带时与传送带速度相等,从D处进入细管到达细管的最高点F水平飞出, 求:
,DEF是光滑细圆管,其中D点与水平面相切,EF是半经为R=0.1m圆弧,乙小球的直经比细管直经略小点,乙小球离开传送带时与传送带速度相等,从D处进入细管到达细管的最高点F水平飞出, 求: