题目内容
（2011?上饶二模）（I）已知金属铯的逸出功为1.9eV，在光电效应实验中，要使铯表面发出的光电子的最大动能为1.0eV，入射光的波长应为
（II）已知氘核质量为2.0136u，中子质量为1.0087u，
He核的质量为3.0150u．
（1）写出两个氘核聚变成
He的核反应方程；
（2）计算上述核反应中释放的核能；
（3）若两氘核以相等的动能0.35MeV做对心碰撞即可发生上述核反应，且释放的核能全部转化为机械能，则反应中生成的
He核和中子的动能各是多少？
4.3×10-9
4.3×10-9
m．（h=6.7х10-34Js）（II）已知氘核质量为2.0136u，中子质量为1.0087u，
|
（1）写出两个氘核聚变成
|
（2）计算上述核反应中释放的核能；
（3）若两氘核以相等的动能0.35MeV做对心碰撞即可发生上述核反应，且释放的核能全部转化为机械能，则反应中生成的
|
分析：（Ⅰ）根据爱因斯坦光电效应方程Ek=hγ-W和c=λγ结合求出入射光的波长．
（Ⅱ）（1）质量数守恒和核电荷数守恒书写核反应方程．
（2）先求出核反应中质量亏损，再由爱因斯坦质能方程，求出核反应中释放的核能；
（3）两氘核对心碰撞过程，遵守动量守恒和能量守恒．生成的
He核和中子的动能之和等于原来的反应动能与释放的核能之和．根据动量守恒和能量守恒列方程，求解
He核和中子的动能．
（Ⅱ）（1）质量数守恒和核电荷数守恒书写核反应方程．
（2）先求出核反应中质量亏损，再由爱因斯坦质能方程，求出核反应中释放的核能；
（3）两氘核对心碰撞过程，遵守动量守恒和能量守恒．生成的
|
|
解答：解：（I）根据爱因斯坦光电效应方程Ek=hγ-W和c=λγ得，
Ek=h
-W
代入解得，λ=4.3×10-9 m．
（II）（1）由质量数守恒和核电荷数守恒，写出核反应方程为：
H+
H→
He+
n
（2）由题给条件得核反应中质量亏损为：
△m=2.0136u×2-（3.0150+1.0087）u=0.0035u
所以释放的核能为
△E=△mc2=931.5×0.0035MeV=3.26 MeV．
因为该反应中释放的核能全部转化为机械能--即转化为He核和中子的动能．
设
He核和中子的质量分别为m1、m2，速度分别为υ1、υ2，
则由动量守恒及能的转化和守恒定律，得
m1υ1-m2υ2=0
Ek1+Ek2=2Ek0+△E
解方程组，可得：
Ek1=
（2Ek0+△E）=
×（2×0.35+3.26）MeV=0.99 MeV，
Ek2=
（2Ek0+△E）=
×（2×0.35+3.26）MeV=2.97 MeV．
故答案为：
（I）4.3×10-9
（II）（1）核反应方程为：
H+
H→
He+
n．
（2）上述核反应中释放的核能为3.26 MeV．
（3）反应中生成的
He核和中子的动能各是0.99 MeV和2.97 MeV．
Ek=h
| c |
| λ |
代入解得，λ=4.3×10-9 m．
（II）（1）由质量数守恒和核电荷数守恒，写出核反应方程为：
|
|
|
|
（2）由题给条件得核反应中质量亏损为：
△m=2.0136u×2-（3.0150+1.0087）u=0.0035u
所以释放的核能为
△E=△mc2=931.5×0.0035MeV=3.26 MeV．
因为该反应中释放的核能全部转化为机械能--即转化为He核和中子的动能．
设
|
则由动量守恒及能的转化和守恒定律，得
m1υ1-m2υ2=0
Ek1+Ek2=2Ek0+△E
解方程组，可得：
Ek1=
| 1 |
| 4 |
| 1 |
| 4 |
Ek2=
| 3 |
| 4 |
| 3 |
| 4 |
故答案为：
（I）4.3×10-9
（II）（1）核反应方程为：
|
|
|
|
（2）上述核反应中释放的核能为3.26 MeV．
（3）反应中生成的
|
点评：光电效应是选修3-5的重点内容，要加强学习，牢固掌握．对于核反应书写核反应方程，要抓住微观粒子的碰撞，相当于弹性碰撞，遵守两大守恒：动量守恒和能量守恒．
练习册系列答案
相关题目
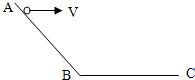（2011?上饶二模）如图所示，AB为斜面，BC水平面．从A点以水平初速度v向右抛出一小球，其第一落点与A的水平距离为s1；从A点以水平初速度2v向右抛出一小球，其第一落点与A的水平距离为s2．不计空气阻力，则s1：s2可能为（ ）
（2011?上饶二模）一弹簧一端固定在倾角为370光滑斜面的底端，另一端拴住的质量m1=4kg的物块P，Q为一重物，已知Q的质量m2=8kg，弹簧的质量不计，劲度系数k=600N/m，系统处于静止，如右图所示．现给Q施加一个方向沿斜面向上的力F，使它从静止开始斜向上做匀加速运动，已知在前0.2s时间内，F为变力，0.2s以后，F为恒力．求力F的最大值与最小值．（g=10m/s2）
（2011?上饶二模）承载着我国载人飞船和空间飞行器交会对接技术的“天宫一号”将于2011年下半年发射，随后将发射“神舟八号”飞船并与“天宫一号”实现交会对接．从此以“天宫一号”为平台开展空间实验室的有关技术验证，假设“天宫一号”和“神舟八号”绕地球做匀速圆周运动轨道如图所示，A代表“天宫一号”，B代表“神舟八号”，虚线为各自的轨道．“天宫一号”和“神舟八号”离地高度分别为h1、h2，运行周期分别为T1、T2，地球可视为质量分布均匀的球体，且忽略自转影响，引力常量为G，则以下说法正确的是（ ）