Question

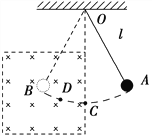
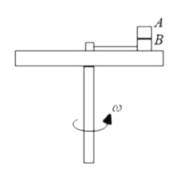
【题目】如图，水平转盘可绕竖直中心轴转动，盘上叠放着质量均为的A、B两个物块，B物块用长为的细线与固定在转盘中心处的力传感器相连，两个物块和传感器的大小均可不计，细线能承受的最大拉力为8N。A、B间的动摩擦因数为0.4，B与转盘间的动摩擦因数为0.1，且可认为最大静摩擦力等于滑动摩擦力。转盘静止时，细线刚好伸直，传感器的读数为零。当转盘以不同的角速度匀速转动时，传感器上就会显示相应的读数F，则下列判断正确的是（　　）

A.当时，随着角速度的增大，力传感器的读数一直增大

B.当时，随着角速度的增大，力传感器的读数一直增大

C.当细线恰好被拉断时，A、B恰好发生相对滑动

D.当时，细线恰好被拉断

Answer 1

【答案】D

【解析】

A．对AB整体分析，当绳子刚有拉力时，根据牛顿第二定律得

即当B物体与转盘将发生滑动时的角速度为

则当时，绳子拉力为0，故A错误；

BCD．当A物体所受的摩擦力大于最大静摩擦力时，A将要脱离B物体，此时的角速度

得

当ω=4rad/s时，此时绳子的张力为

则

接下来随角速度的增大，Ａ脱离Ｂ物体。只有Ｂ物体作匀速圆周运动，当拉力最大时的角速度为ω3，根据牛顿第二定律得

则

所以当细线中的拉力F=6N时，A与B即将相对滑动，当转盘的角速度为6rad/s时，细线拉力达到最大，当转盘的角速度大于6rad/s时，绳子断裂，故BC错误，D正确。

故选D。