题目内容
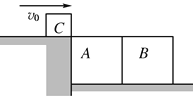
【题目】如图所示，水平传送带AB长L=6m，以v0=3m/s的恒定速度转动．水平光滑台面与传送带平滑连接于B点，竖直平面内的半圆形光滑轨道半径R=0.4m，与水平台面相切于C点．一质量m=1kg的物块(可视为质点)，从A点无初速释放，当它运动到A、B中点位置时，刚好与传送带保持相对静止．重力加速度g=10m/s2．试求：
⑴物块与传送带之间的动摩擦因数
；
⑵物块刚滑过C点时对轨道的压力FN；
⑶物块在A点至少要具有多大的速度，才能通过半圆形轨道的最高点D(结果可用根式表示) ．
【答案】⑴
⑵
【解析】⑴对物块，由静止开始做匀加速直线运动，由牛顿第二定律和运动学公式有
(2分)
(2分)
解得(1分)
⑵物块刚滑过C点时的速度vC=vB=3m/s
在C点，有
(2分)
解得FN=32.5N (1分)
由牛顿第三定律知，物块对轨道的压力大小为32.5N，方向竖直向下． (1分)
⑶物块经过半圆轨道最高点D的最小速度为
(1分)
由C到D的过程中，由动能定理有
(1分)
解得
(1分)
可见，物块从A到B的全过程中一直做匀减速直线运动，到达B端的速度至少为
(1分)
由⑴问可知，物块在传送带上减速运动时的加速度大小a=1.5m/s2
由运动学公式有
(1分)
解得(1分)
练习册系列答案
相关题目
