题目内容
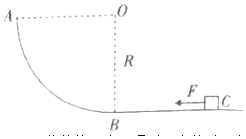
【题目】如图所示，在水平地面上固定一个光滑管道ABCDE，圆形管道的半径为R=0.4m,竖直管道AE与圆形管道相切于与圆心等高的B点，圆形管道最低点C与竖直管道末端E处于同一高度。现将一质量m=0.1kg、直径略小于管道内径的小球(可看做质点)从管口A处由静止释放，小球经过圆形管道最高点D时恰好对管道没有压力，最终小球由管道末端E下落，重力加速度取g=10m/s2,则竖直管道AB的长度和小球在C点时对管道压力的大小分别为( )
A. 0.6m 12N B. 1.2m 12N C. 1.2m 6N D. 0.6m 6N
【答案】D
【解析】设AB的长度为L，由于小球经过圆形管道最高点D时恰好对管道没有压力，则小球在最高点D应满足：
，小球从A运动至D的过程，由动能定理有：
，可得：L=0.6m；小球从C运动至D过程，由机械能守恒定律有：
，设在C点时管道对小球的支持力为FN，由牛顿第二定律有：
，可得：FN=6N，由牛顿第三定律可得，小球对管道的压力为6N，方向竖直向下，选项D正确。故选D。
练习册系列答案
相关题目
