题目内容
13. 用绝缘细线悬挂一个质量为m,带电量为+q的小球,让它处于图所示的磁感应强度为B的匀强磁场中,由于磁场的运动,小球静止在如图位置,这时悬线与竖直方向的夹角为α,且细线的拉力不为0,则磁场的运动速度大小和方向是( )
用绝缘细线悬挂一个质量为m,带电量为+q的小球,让它处于图所示的磁感应强度为B的匀强磁场中,由于磁场的运动,小球静止在如图位置,这时悬线与竖直方向的夹角为α,且细线的拉力不为0,则磁场的运动速度大小和方向是( )| A. | v=$\frac{mg}{Bq}$,水平向右 | B. | v=$\frac{mgsinα}{Bq}$,沿线向上 | ||
| C. | v=$\frac{mgtanα}{Bq}$,竖直向上 | D. | v=$\frac{mgtanα}{Bq}$,竖直向下 |
分析 根据磁场的运动方向得出小球相对磁场的运动方向,根据左手定则得出洛伦兹力的方向,从而结合共点力平衡分析求解.
解答 解:若磁场向右运动,小球相对磁场向左运动,小球所受的洛伦兹力方向竖直向下,小球受重力、洛伦兹力和拉力不可能平衡,故A错误.
B、若磁场沿线向上运动,则小球相对磁场沿线向下,小球所受的洛伦兹力方向垂直细线斜向上,根据共点力平衡有:mgsinα=qvB,解得v=$\frac{mgsinα}{qB}$,故B正确.
C、若磁场竖直向上运动,则小球相对磁场向下运动,小球所受的洛伦兹力方向水平向右,根据共点力平衡有:mgtanα=qvB,解得v=$\frac{mgtanα}{qB}$,故C正确.
D、若磁场竖直向下运动,则小球相对磁场向上运动,小球所受的洛伦兹力方向水平向左,小球受重力、洛伦兹力、拉力不可能平衡,故D错误.
故选:BC.
点评 考查左手定则与平衡方程的应用,注意相对运动理解,突出小球相对磁场的运动方向是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3. “飞车走壁”是一种传统的杂技艺术,演员骑车在倾角很大的桶 面上做圆周运动而不掉下来.如图所示,已知桶壁的倾角为θ,车和人的总质量为m,做圆周运动的半径为r,若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )
“飞车走壁”是一种传统的杂技艺术,演员骑车在倾角很大的桶 面上做圆周运动而不掉下来.如图所示,已知桶壁的倾角为θ,车和人的总质量为m,做圆周运动的半径为r,若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )
 “飞车走壁”是一种传统的杂技艺术,演员骑车在倾角很大的桶 面上做圆周运动而不掉下来.如图所示,已知桶壁的倾角为θ,车和人的总质量为m,做圆周运动的半径为r,若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )
“飞车走壁”是一种传统的杂技艺术,演员骑车在倾角很大的桶 面上做圆周运动而不掉下来.如图所示,已知桶壁的倾角为θ,车和人的总质量为m,做圆周运动的半径为r,若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )| A. | 人和车的速度为$\sqrt{grtanθ}$ | B. | 桶面对车的弹力为$\frac{mg}{sinθ}$ | ||
| C. | 桶面对车的弹力为$\frac{mg}{cotθ}$ | D. | 人和车的速度为$\sqrt{grsinθ}$ |
8.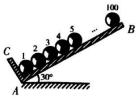 如图所示,100个大小相同、质量均为M的光滑小球,静止放置于两个相互垂直挡板上,平面AB与水平面夹角为30°,则( )
如图所示,100个大小相同、质量均为M的光滑小球,静止放置于两个相互垂直挡板上,平面AB与水平面夹角为30°,则( )
 如图所示,100个大小相同、质量均为M的光滑小球,静止放置于两个相互垂直挡板上,平面AB与水平面夹角为30°,则( )
如图所示,100个大小相同、质量均为M的光滑小球,静止放置于两个相互垂直挡板上,平面AB与水平面夹角为30°,则( )| A. | 第2个小球受4个力作用 | |
| B. | 第8个小球受力个数可能小于4 | |
| C. | 斜面对第31个小球的支持力为$\frac{Mg}{2}$ | |
| D. | 第90个小球对第91个小球弹力大小为5Mg |
18.将3个阻值均为6Ω的电阻同时使用,采用不同的方式进行连接,可能获得的总电阻是( )
| A. | 2Ω | B. | 3Ω | C. | 9Ω | D. | 18Ω |
5. 如图所示,放置在水平地面上的支架质量为M,支架顶端用细线拴着的摆球质量为m,现将摆球拉起使细线水平且处于伸直状态,然后由静止释放摆球,摆球在运动过程中,不会与支架相碰,支架始终不动,以下判断正确的是( )
如图所示,放置在水平地面上的支架质量为M,支架顶端用细线拴着的摆球质量为m,现将摆球拉起使细线水平且处于伸直状态,然后由静止释放摆球,摆球在运动过程中,不会与支架相碰,支架始终不动,以下判断正确的是( )
 如图所示,放置在水平地面上的支架质量为M,支架顶端用细线拴着的摆球质量为m,现将摆球拉起使细线水平且处于伸直状态,然后由静止释放摆球,摆球在运动过程中,不会与支架相碰,支架始终不动,以下判断正确的是( )
如图所示,放置在水平地面上的支架质量为M,支架顶端用细线拴着的摆球质量为m,现将摆球拉起使细线水平且处于伸直状态,然后由静止释放摆球,摆球在运动过程中,不会与支架相碰,支架始终不动,以下判断正确的是( )| A. | 在释放瞬间,支架对地面压力为(M+m)g | |
| B. | 摆球到达最低点时,地面对支架的摩擦力方向向左 | |
| C. | 摆球到达最低点时,支架对地面压力为(M+m)g | |
| D. | 摆球到达最低点时,支架对地面压力为(M+3m)g |
 如图所示,两块相同的竖直挡板A、B之间有质量均为m的四块相同的砖,用两个大小均为F的水平力压木板,使砖静止不动.设所有接触面之间的动摩擦因数都为μ,那么1、2 两块砖之间的摩擦力大小为mg,2、3两块砖之间的摩擦力大小为0.
如图所示,两块相同的竖直挡板A、B之间有质量均为m的四块相同的砖,用两个大小均为F的水平力压木板,使砖静止不动.设所有接触面之间的动摩擦因数都为μ,那么1、2 两块砖之间的摩擦力大小为mg,2、3两块砖之间的摩擦力大小为0.



 以下是小丽同学在“探究共点力作用下物体的平衡条件”实验中的操作步骤,请将步骤补充完整.
以下是小丽同学在“探究共点力作用下物体的平衡条件”实验中的操作步骤,请将步骤补充完整. 如图,光滑水平地面上有平板A,其上端左侧边缘有一个小木块B(可视为质点),开始均处于静止状态,平板A右侧有竖直固定的墙面,且距离平板A足够远.现有质量为m=0.01kg的子弹C以速度v0=200m/s水平射入木块B并一起运动,子弹进入木块的时间极短,可以忽略不计,mA=1.5kg,mB=0.5kg,A与B间的滑动摩擦因数μ=0.5,木板撞墙前已经与木块共速.求;
如图,光滑水平地面上有平板A,其上端左侧边缘有一个小木块B(可视为质点),开始均处于静止状态,平板A右侧有竖直固定的墙面,且距离平板A足够远.现有质量为m=0.01kg的子弹C以速度v0=200m/s水平射入木块B并一起运动,子弹进入木块的时间极短,可以忽略不计,mA=1.5kg,mB=0.5kg,A与B间的滑动摩擦因数μ=0.5,木板撞墙前已经与木块共速.求;