Question

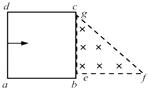
【题目】质谱仪原理如图所示，a为粒子加速器，电压为U1；b为速度选择器，磁场与电场正交，磁感应强度为B1 ， 板间距离为d；c为偏转分离器，磁感应强度为B2 ． 今有一质量为m、电荷量为+e的正电子（不计重力），经加速后，该粒子恰能通过速度选择器，粒子进入分离器后做半径为R的匀速圆周运动．求：

（1）粒子射出加速器时的速度v为多少？
（2）速度选择器的电压U2为多少？
（3）粒子在B2磁场中做匀速圆周运动的半径R为多大？

Answer 1

【答案】
（1）解：粒子经加速电场U1加速，获得速度为v，由动能定理可知：

eU1= mv2

解得v=

答：粒子射出加速器时的速度v为 ；

（2）解：在速度选择器中作匀速直线运动，电场力与洛仑兹力平衡得：eE=evB1

即

解得：U2=B1dv=B1d

答：速度选择器的电压B1d ；

（3）解：在B2中作圆周运动，洛仑兹力提供向心力，qvB2=m

解得：R=

答：粒子在B2磁场中做匀速圆周运动的半径为 ．

【解析】（1）根据动能定理qU1= mv2求出粒子的速度v．（2）在速度选择器中作匀速直线运动，电场力与洛仑兹力平衡，根据Eq=qvB1求出电压U2．（3）根据洛仑兹力提供向心力，qvB2= ，求出粒子在B2磁场中做匀速圆周运动的半径R．
【考点精析】根据题目的已知条件，利用洛伦兹力和感应电流的方向的相关知识可以得到问题的答案，需要掌握洛伦兹力始终垂直于v的方向，所以洛伦兹力一定不做功；通电导体在磁场中受力方向：跟电流方向和磁感线方向有关．（左手定则）．