题目内容
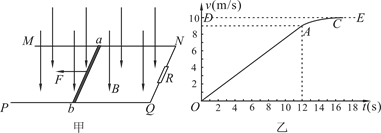
(18分)如图所示,相距为R的两块平行金属板M、 N正对着放置,S1、S2分别为M、N板上的小孔,S1、S2、O三点共线,它们的连线垂直M、N,且S2O=R.以O为圆心、R为半径的圆形区域内存在磁感应强度为B、方向垂直纸面向外的匀强磁场.D为收集板,板上各点到O点的距离以及板两端点的距离都为2R,板两端点的连线垂直M、N板.质量为m、带电量为+q的粒子经S1进入M、N间的电场后,通过S2进入磁场.粒子在S1处的速度以及粒子所受的重力均不计.

(1)M、N间的电压为U时,求粒子进入磁场时速度的大小v;
(2)若粒子恰好打在收集板D的中点上,求M、N间的电压值U0;
(3)当M、N间的电压不同时,粒子从S1到打在D上经历的时间t会不同,求
t的最小值.

(1)M、N间的电压为U时,求粒子进入磁场时速度的大小v;
(2)若粒子恰好打在收集板D的中点上,求M、N间的电压值U0;
(3)当M、N间的电压不同时,粒子从S1到打在D上经历的时间t会不同,求
t的最小值.
(1)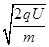 (2)
(2)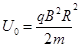 (3)
(3)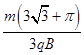
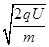 (2)
(2)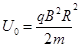 (3)
(3)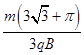
试题分析: (1)粒子从S1到达S2的过程中,根据动能定理得
qU=
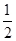 mv2 ① 2分
mv2 ① 2分解得粒子进入磁场时速度的大小
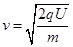 1分
1分(2)粒子进入磁场后在洛伦兹力作用下做匀速圆周运动,有
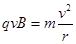 ② 2分
② 2分由①②得,加速电压U与轨迹半径r的关系为
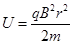 1分
1分当粒子打在收集板D的中点时,粒子在磁场中运动的半径
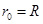 1分
1分对应电压
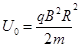 1分
1分(3)M、N间的电压越大,粒子进入磁场时的速度越大,粒子在极板间经历的时间越短,同时在磁场中运动轨迹的半径越大,在磁场中运动的时间也会越短,出磁场后匀速运动的时间也越短,所以当粒子打在收集板D的右端时,对应时间t最短。
根据几何关系可以求得,对应粒子在磁场中运动的半径r=
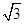 R 2分
R 2分由②得粒子进入磁场时速度的大小
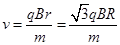 1分
1分粒子在电场中经历的时间
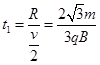 2分
2分粒子在磁场中经历的时间
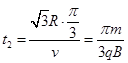 2分
2分粒子出磁场后做匀速直线运动经历的时间
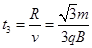 2分
2分粒子从S1到打在收集板D上经历的最短时间为t=t1+t2+t3=
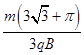 1分
1分
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
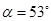 ,轨道上端接一只阻值为R=0.4
,轨道上端接一只阻值为R=0.4 的电阻器,在导轨间存在垂直于导轨平面的匀强磁场,磁场的磁感应强度B=0.5 T,两轨道之间的距离为L=40cm,且轨道足够长,电阻不计。现将一质量为m="3" g,有效电阻为r=1.0
的电阻器,在导轨间存在垂直于导轨平面的匀强磁场,磁场的磁感应强度B=0.5 T,两轨道之间的距离为L=40cm,且轨道足够长,电阻不计。现将一质量为m="3" g,有效电阻为r=1.0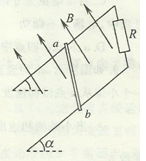
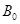 =50T,已知两板间距离d=0.3m,电场强度E=50V/m,M板中心上有一小孔P,在P正上方h=5cm处的O点,一带电油滴自由下落,穿过小孔后进入两板间,若油滴在t=0时刻进入两板间,最后恰好从N板边缘水平飞出。已知油滴的质量 m=10
=50T,已知两板间距离d=0.3m,电场强度E=50V/m,M板中心上有一小孔P,在P正上方h=5cm处的O点,一带电油滴自由下落,穿过小孔后进入两板间,若油滴在t=0时刻进入两板间,最后恰好从N板边缘水平飞出。已知油滴的质量 m=10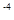 kg,电荷量q=+2×10
kg,电荷量q=+2×10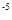 C(不计空气阻力。重力加速度取g=10m/s2,取π=3)求:
C(不计空气阻力。重力加速度取g=10m/s2,取π=3)求: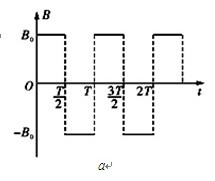
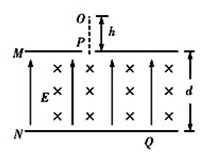
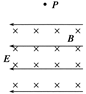
 中,
中, 轴左侧有沿
轴左侧有沿 轴正向的匀强电场,场强大小为E;
轴正向的匀强电场,场强大小为E; 时刻,从
时刻,从
 沿x轴正向进入电场,从y轴上Q点离开电场时速度方向与y轴负向夹角
沿x轴正向进入电场,从y轴上Q点离开电场时速度方向与y轴负向夹角 ,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的有界匀强磁场区域(图中未画出),磁场磁感应强度大小
,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的有界匀强磁场区域(图中未画出),磁场磁感应强度大小 ,粒子能从坐标原点O沿x轴负向再进入电场.不计粒子重力,求:
,粒子能从坐标原点O沿x轴负向再进入电场.不计粒子重力,求: