��Ŀ����
����Ŀ����ͼ��ʾ�������Ƿ���ˮƽ�����ϵ�����С��飨����Ϊ�ʵ㣩�������ֱ�Ϊm1��2kg��m2��3kg��������Ķ�Ħ��������ͬ����ʼ����L��170m�����߷ֱ���v1��10m/s��v2��2m/s�ij��ٶ�ͬʱ�����˶�������t��20s��ʱ�����߷�����ײ�������������Ķ�Ħ����������ijͬѧ�ⷨ���£�
��Ħ��������ͬ����������Ħ���������¼��ٶȵĴ�С����ͬ�ģ���ţ�ٵڶ����ɵõ����ٶȵĴ�С��a����g������������t��20s��ʱ�����˶�·�̷ֱ�Ϊs1��s2�����У�![]() ��
��![]() �����ǵ�s1+s2��L�������������������Ϊ��ͬѧ�Ľ���Ƿ�������������������������������������˵�����ɣ��������Լ��ķ��������ȷ�����
�����ǵ�s1+s2��L�������������������Ϊ��ͬѧ�Ľ���Ƿ�������������������������������������˵�����ɣ��������Լ��ķ��������ȷ�����

���𰸡���ͬѧ�ⷨ����������Ϊδ���������Ƿ�ֹͣ�� ���������Ķ�Ħ������Ϊ0.02��
��������
��ͬѧ�Ľ���� ��
��Ϊ��ʽ�������������ݺ���a��0.175m/s2
����ʱ��t��20s���������ٶȷֱ�Ϊ v'1��v1��at��v'2��v2��at
�������ݵ� v'1��6.5m/s��v'2����1.5m/s��v'2��0�������������20s֮ǰ���Ѿ�ֹͣ�˶����ʸ�ͬѧ�������
��ȷ������2ֹͣ�˶�ǰ���еľ���![]()
������֮ǰ��λ�ƹ�ϵs1+s2��L
����Ϊ![]()
�������ݵã�100a2��15a��1��0
��� a��0.2m/s2 ��a����0.05m/s2 ����ȥ����
����a����g��������0.02��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ����6�֣�ij����С���ͬѧ�����һ���������С��ͨ����������͵�ʱ���ٶȵ�ʵ�顣���������У����С����ѹ��ʽ���̳ӡ�������ģ������Բ�����ֵİ뾶ΪR=0.20m����

���������գ�
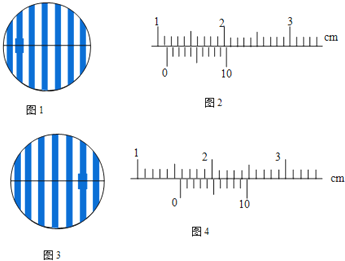
��1����������ģ�������������̳��ϣ���ͼ��a����ʾ�����̳ӵ�ʾ��Ϊ1.00kg��
��2�������С�������ڰ�����ģ������͵�ʱ�����̳ӵ�ʾ����ͼ��b����ʾ����ʾ��Ϊ_____kg;
��3����С���Ӱ�����ģ����ijһλ���ͷţ�С��������͵������һ�࣬�˹��������̳ӵ����ʾ��Ϊm����δ�ͬһλ���ͷ�С������¼���ε�mֵ���±���ʾ��
��� | 1 | 2 | 3 | 4 | 5 |
m��kg�� | 1.80 | 1.75 | 1.85 | 1.75 | 1.90 |
��4�������������ݣ������С��������������͵�ʱ���ŵ�ѹ��Ϊ_____N��С��ͨ����͵�ʱ���ٶȴ�СΪ_______m/s�����������ٶȴ�Сȡ9.80m/s2 ������������2λ��Ч���֣�