��Ŀ����
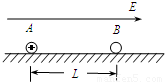
�ڹ⻬ˮƽ���Ͼ�ֹ��A��B����С����Ϊ�ʵ㣩��������Ϊm��A��������Ϊq������ɣ�B���磬�������ΪL����t=0ʱ�̿�ʼ������С�����ڵ�ˮƽ�ռ��ڼ�һ��Χ�㹻�����ǿ�糡���糡ǿ��ΪE��������A��B���������ƽ�����ң���ͼ��ʾ��A���ڵ糡���������ɾ�ֹ��ʼ��ֱ���˶�������B������ȫ������ײ�����������ײ��Զ���ڵ糡��������ʱ�伫�̣�ÿ����ײ������A��B֮��û�е����ת�ƣ��Ҳ����ǿ���������������������������
��1��С��A���ʱ����С��B������һ����ײ��
��2��С��A��С��B������һ����ײ��˲��A��B������ٶȴ�С�ֱ��Ƕ��٣�
��3���ڶ�����ײ���־��ʱ�䷢����������ײ��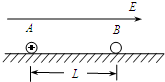
��1��С��A���ʱ����С��B������һ����ײ��
��2��С��A��С��B������һ����ײ��˲��A��B������ٶȴ�С�ֱ��Ƕ��٣�
��3���ڶ�����ײ���־��ʱ�䷢����������ײ��

��1��С��A�ڵ糡�������������ȼ���ֱ���˶���
L=
at12
a=
��
��ã�t1=
��
��2��С��A��С��B������ȫ������ײ����A����ǰ�ٶ�ΪvA1�������ٶ�ΪvA1'��B����ǰ�ٶ�Ϊ0�������ٶ�ΪvB1'��
m vA1=m vA1'+m vB1'
m vA12=
m vA1��2+
m vB1��2
�����ã�vA1'=0
vB1'=vA1
vA1=at1=
���ԣ�vA1'=0��vB1'=
��3����һ����ײ��С��A�����ٶ�Ϊ0���ȼ���ֱ���˶���С��B�� vB1'���ٶ�������ֱ���˶�����С�����ڶ�����ײ�������ǣ���С��λ����ȣ�
��ڶ�����ײA����ǰ�ٶ�ΪvA2�������ٶ�ΪvA2'��B����ǰ�ٶ�ΪvB2�������ٶ�ΪvB2'��
vA2=at2=
t2
vB2=vB1'=
��
at22=vB2t2������
����ã�t2=2
vA2=at2=2
��
m vA2+m vB2=m vA2'+m vB2'
mvA22+
mvB22=
mvA2��2+
mvB2��2
�����ã�vA2'=vB2
vB2'=vA2
���ԣ�vA2'=
vB2'=2
�ڶ�����ײ��С��A�����ٶ�Ϊ
���ȼ���ֱ���˶���С��B�� vB2'���ٶ�������ֱ���˶�����С������������ײ�������ǣ���С��λ����ȣ�
���������ײA����ǰ�ٶ�ΪvA3�������ٶ�ΪvA3'��B����ǰ�ٶ�ΪvB3�������ٶ�ΪvB3'��
vB3=vB2'=2
t3+
at32=vB3t3
��ã�t3=2
������������������
����ɵڶ�����ײ���־�t3=2
��ʱ�䷢����������ײ����ʱ�䲻�ٷ����仯��
�𣺣�1��С��A��С��B������һ����ײ�����ʱ��Ϊt1=
��
��2��С��A��С��B������һ����ײ��˲��A��B������ٶȴ�С�ֱ���0��
��
��3���ڶ�����ײ���־�t3=2
������������ײ��
L=
| 1 |
| 2 |
a=
| qE |
| m |
��ã�t1=
|
��2��С��A��С��B������ȫ������ײ����A����ǰ�ٶ�ΪvA1�������ٶ�ΪvA1'��B����ǰ�ٶ�Ϊ0�������ٶ�ΪvB1'��
m vA1=m vA1'+m vB1'
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
�����ã�vA1'=0
vB1'=vA1
vA1=at1=
|
���ԣ�vA1'=0��vB1'=
|
��3����һ����ײ��С��A�����ٶ�Ϊ0���ȼ���ֱ���˶���С��B�� vB1'���ٶ�������ֱ���˶�����С�����ڶ�����ײ�������ǣ���С��λ����ȣ�
��ڶ�����ײA����ǰ�ٶ�ΪvA2�������ٶ�ΪvA2'��B����ǰ�ٶ�ΪvB2�������ٶ�ΪvB2'��
vA2=at2=
| qE |
| m |
vB2=vB1'=
|
| 1 |
| 2 |
����ã�t2=2
|
|
m vA2+m vB2=m vA2'+m vB2'
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
�����ã�vA2'=vB2
vB2'=vA2
���ԣ�vA2'=
|
vB2'=2
|
�ڶ�����ײ��С��A�����ٶ�Ϊ
|
���������ײA����ǰ�ٶ�ΪvA3�������ٶ�ΪvA3'��B����ǰ�ٶ�ΪvB3�������ٶ�ΪvB3'��
vB3=vB2'=2
|
|
| 1 |
| 2 |
��ã�t3=2
|
����ɵڶ�����ײ���־�t3=2
|
�𣺣�1��С��A��С��B������һ����ײ�����ʱ��Ϊt1=
|
��2��С��A��С��B������һ����ײ��˲��A��B������ٶȴ�С�ֱ���0��
|
��3���ڶ�����ײ���־�t3=2
|

��ϰ��ϵ�д�
 ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
�����Ŀ
�ڹ⻬ˮƽ���Ͼ�ֹ��һ��С�� ,��һ��С��
,��һ��С�� ��ijһˮƽ�ٶ���
��ijһˮƽ�ٶ��� ��������������
�������������� ����˶���������ǰ�ķ����෴��������˵����ȷ���� (����)
����˶���������ǰ�ķ����෴��������˵����ȷ���� (����)
A������ ��Ķ�������ײ�� ��Ķ�������ײ�� ��Ķ����� ��Ķ����� |
B������ײ������ ��B����Ķ����仯����ͬ ��B����Ķ����仯����ͬ |
C����ײ�� ��Ķ�������ײǰ ��Ķ�������ײǰ �Ķ���С �Ķ���С |
D����ײ�� ��Ķ��ܱ���ײ�� ��Ķ��ܱ���ײ�� ��Ķ��ܴ� ��Ķ��ܴ� |
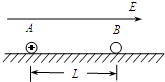 �ڹ⻬ˮƽ���Ͼ�ֹ��A��B����С����Ϊ�ʵ㣩��������Ϊm��A��������Ϊq������ɣ�B���磬�������ΪL����t=0ʱ�̿�ʼ������С�����ڵ�ˮƽ�ռ��ڼ�һ��Χ�㹻�����ǿ�糡���糡ǿ��ΪE��������A��B���������ƽ�����ң���ͼ��ʾ��A���ڵ糡���������ɾ�ֹ��ʼ��ֱ���˶�������B������ȫ������ײ�����������ײ��Զ���ڵ糡��������ʱ�伫�̣�ÿ����ײ������A��B֮��û�е����ת�ƣ��Ҳ����ǿ���������������������������
�ڹ⻬ˮƽ���Ͼ�ֹ��A��B����С����Ϊ�ʵ㣩��������Ϊm��A��������Ϊq������ɣ�B���磬�������ΪL����t=0ʱ�̿�ʼ������С�����ڵ�ˮƽ�ռ��ڼ�һ��Χ�㹻�����ǿ�糡���糡ǿ��ΪE��������A��B���������ƽ�����ң���ͼ��ʾ��A���ڵ糡���������ɾ�ֹ��ʼ��ֱ���˶�������B������ȫ������ײ�����������ײ��Զ���ڵ糡��������ʱ�伫�̣�ÿ����ײ������A��B֮��û�е����ת�ƣ��Ҳ����ǿ��������������������������� ��ͼ��ʾ���ڹ⻬ˮƽ���Ͼ�ֹ��һ������ΪM=5kg�ij�����ľ��A��ľ�����˾�ֹ������һ����Ϊm=2kg�����B����֪AB֮�䶯Ħ��������=0.5������ʵ�鷢�ֵ������Bʩ��һ����СΪ16Nˮƽ���ҵ�����F��2s���B������ľ����Ҷˣ�gȡ10m/s2����
��ͼ��ʾ���ڹ⻬ˮƽ���Ͼ�ֹ��һ������ΪM=5kg�ij�����ľ��A��ľ�����˾�ֹ������һ����Ϊm=2kg�����B����֪AB֮�䶯Ħ��������=0.5������ʵ�鷢�ֵ������Bʩ��һ����СΪ16Nˮƽ���ҵ�����F��2s���B������ľ����Ҷˣ�gȡ10m/s2���� ,��һ��С��
,��һ��С�� ��ijһˮƽ�ٶ���
��ijһˮƽ�ٶ���