题目内容
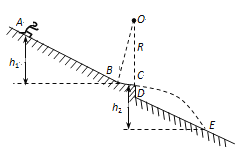
【题目】跳台滑雪是冬奥会的比赛项目之一,如图为简化后的跳台滑雪的雪道示意图。助滑道AB为斜坡,底端通过一小段圆弧BC与水平跳台平滑连接。一滑雪运动员从A点由静止滑下,通过C点水平飞出,落到着陆坡DE上。已知运动员与滑雪装备总质量为80kg,AC间的竖直高度差h1=40m,BC段圆弧半径R=10m,CE间的竖直高度差h2=80m、水平距离x=100m。不计空气阻力,取g=10m/s2。求:
(1)运动员到达C点时的速度大小;
(2)运动员到达C点时对滑道压力的大小;
(3)运动员由A滑到C的过程中,克服雪道阻力做了多少功?
【答案】(1)25m/s(2)5800N(3)7000J
【解析】
(1)运动员在空中飞行的时间,由:![]()
得:t=4s
运动员通过C点的速度大小,由![]()
解得:![]()
(2)运动员通过的C点是在BC段圆周运动的最低点,由牛顿第二定律可得:![]()
解得:FN=5800N
由牛顿第三定律可知:运动员对滑道的压力大小:FN′=5800N
(3)运动员从A到C运动过程中,应用动能定理:![]()
解得:Wf=7000J
所以从A到C运动过程中,克服雪道阻力做了7000J的功

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目