题目内容
 如图所示,同一平面内有两根互相平行的长直导线甲和乙,通有大小均为I且方向相反的电流,a、b两点与两导线共面,其连线与导线垂直,a、b到两导线中点O的连线长度和甲乙间距离均相等.已知直线电流I 产生的磁场中磁感应强度的分布规律是B=K
如图所示,同一平面内有两根互相平行的长直导线甲和乙,通有大小均为I且方向相反的电流,a、b两点与两导线共面,其连线与导线垂直,a、b到两导线中点O的连线长度和甲乙间距离均相等.已知直线电流I 产生的磁场中磁感应强度的分布规律是B=K| I | r |
分析:由安培定则判断出甲乙两导线在O点产生的磁场方向,然后求出各导线在O点产生的磁感应强度大小;由安培定则及磁场的叠加原理求出a点的磁感应强度;求出甲在乙处产生的磁感应强度,最后由F=BIL求出乙受到的安培力.
解答:解:设两导线间的距离是L,则由题意知:ao=bo=L;
由安培定则可知,甲乙两电流在O点产生的磁场方向都垂直于纸面向里,
两导线到O点的距离均为
,∵B=k
,O点磁感应强度的大小为B0,
∴B0=Ba+Bb=k
+k
=k
①,
由安培定则可知,甲在a处产生的磁场垂直于纸面向外,
乙在a处产生的磁场垂直于纸面向里,则a处的磁感应强度:
Ba=B甲+B乙=k
-k
=
k
②,
由①②可得:Ba=
;
甲在乙处产生的磁感应强度:
B=k
=
,单位长度l=1m的乙导线受到的安培力:
F=BIl=
×I×1=
B0I;
故答案为:
;
B0I.
由安培定则可知,甲乙两电流在O点产生的磁场方向都垂直于纸面向里,
两导线到O点的距离均为
| L |
| 2 |
| I |
| r |
∴B0=Ba+Bb=k
| I | ||
|
| I | ||
|
| 4I |
| L |
由安培定则可知,甲在a处产生的磁场垂直于纸面向外,
乙在a处产生的磁场垂直于纸面向里,则a处的磁感应强度:
Ba=B甲+B乙=k
| I | ||
|
| I | ||
(L+
|
| 4 |
| 3 |
| I |
| L |
由①②可得:Ba=
| B0 |
| 3 |
甲在乙处产生的磁感应强度:
B=k
| I |
| L |
| B0 |
| 4 |
F=BIl=
| B0 |
| 4 |
| 1 |
| 4 |
故答案为:
| 1 |
| 3 |
| 1 |
| 4 |
点评:本题是一道信息给予题,认真审题,知道磁感应强度的计算公式、熟练应用安培定则、磁场的叠加原理即可正确解题.

练习册系列答案
相关题目
 如图所示,同一平面内有两根固定的相互平行的长直导线甲和乙,现通有大小相等方向相反的电流.a、b两点与两导线共面.其中a点与两导线间距离均为r,b点在导线乙的右侧,与乙距离也为r.测得a点磁感应强度的大小为B,则去掉导线甲后,b点的磁感应强度方向和大小为( )
如图所示,同一平面内有两根固定的相互平行的长直导线甲和乙,现通有大小相等方向相反的电流.a、b两点与两导线共面.其中a点与两导线间距离均为r,b点在导线乙的右侧,与乙距离也为r.测得a点磁感应强度的大小为B,则去掉导线甲后,b点的磁感应强度方向和大小为( )| A、垂直纸面向外,3B | ||
| B、垂直纸面向外,2B | ||
| C、垂直纸面向外,B | ||
D、垂直纸面向外,
|
 如图所示,同一平面内有两根互相平行的长直导线1和2,通有大小相等、方向相反的电流,a、b两点与两导线共面,a点在两导线的中间与两导线的距离均为r,b点在导线2右侧,与导线2的距离也为r.现测得a点磁感应强度的大小为B,则去掉导线1后,b点的磁感应强度方向和大小( )
如图所示,同一平面内有两根互相平行的长直导线1和2,通有大小相等、方向相反的电流,a、b两点与两导线共面,a点在两导线的中间与两导线的距离均为r,b点在导线2右侧,与导线2的距离也为r.现测得a点磁感应强度的大小为B,则去掉导线1后,b点的磁感应强度方向和大小( ) 如图所示,同一平面内的三条平行导线串有两个最阻R和r,导体棒PQ与三条导线接触良好;匀强磁场的方向垂直纸面向里.导体棒的电阻可忽略.当导体棒向左滑动时,下列说法正确的是( )
如图所示,同一平面内的三条平行导线串有两个最阻R和r,导体棒PQ与三条导线接触良好;匀强磁场的方向垂直纸面向里.导体棒的电阻可忽略.当导体棒向左滑动时,下列说法正确的是( )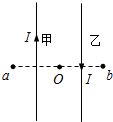 如图所示,同一平面内有两根互相平行的长直导线甲和乙,通有大小均为I=5A且方向相反的电流,a、b两点与两导线共面,其连线与导线垂直,a、b到两导线中点O的连线长度和甲乙间距离均相等.已知直线电流I 产生的磁场中磁感应强度的分布规律是
如图所示,同一平面内有两根互相平行的长直导线甲和乙,通有大小均为I=5A且方向相反的电流,a、b两点与两导线共面,其连线与导线垂直,a、b到两导线中点O的连线长度和甲乙间距离均相等.已知直线电流I 产生的磁场中磁感应强度的分布规律是