题目内容
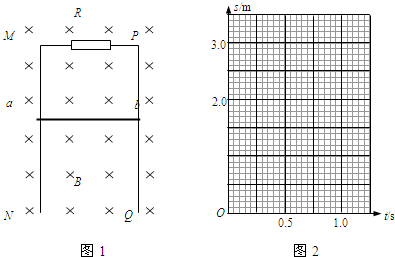
 (2008?崇文区一模)一列沿x轴方向传播的简谐横波,t=0时刻的波形如图中实线所示,t=0.2s时刻的波形为如图虚线所示,则( )
(2008?崇文区一模)一列沿x轴方向传播的简谐横波,t=0时刻的波形如图中实线所示,t=0.2s时刻的波形为如图虚线所示,则( )分析:简谐波传播时,波形向前平移,由波形的平移法分析波的传播方向.根据两个时刻波形关系,确定时间与周期的关系,得到周期的通项,再求解特殊值.再求解频率和波速的通项,分析特殊值.
解答:解:
A、由波形的平移法分析波可能向右传播,也可能向左传播.故A错误.
B、若波向右传播,则时间△t=(n+
)T,得到周期T=
=
s,n=0,1,2…;
同理,若波向左传播,周期T=
s,n=0,1,2…;由于n是整数,T可能等于为
s.故B正确.
C、频率的通项为:波向右传播时,f=
Hz,波向左传播时,f=
Hz,n=0,1,2…;由于n是整数,f不可能等于
Hz.故C错误.
D、由图读出波长为λ=1.2m.波速的通项为:向左:v=
(4n+1)m/s,n=0,1,2…;向右:v=
(4n+3)m/s,n=0,1,2…;可见,当v=20m/s.n不是整数,故D错误.
故选B
A、由波形的平移法分析波可能向右传播,也可能向左传播.故A错误.
B、若波向右传播,则时间△t=(n+
| 3 |
| 4 |
| 4?△t |
| 4n+3 |
| 0.8 |
| 4n+3 |
同理,若波向左传播,周期T=
| 0.8 |
| 4n+1 |
| 4 |
| 15 |
C、频率的通项为:波向右传播时,f=
| 4n+3 |
| 0.8 |
| 4n+1 |
| 0.8 |
| 4 |
| 5 |
D、由图读出波长为λ=1.2m.波速的通项为:向左:v=
| 3 |
| 2 |
| 3 |
| 2 |
故选B
点评:本题运用数学知识得到波的周期、频率和波速通项的能力,要考虑波的周期性和双向性.

练习册系列答案
相关题目

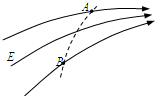 (2008?崇文区一模)某电场的部分电场线如图所示,A、B是一带电粒子仅在电场力作用下运动轨迹(图中虚线)上的两点,下列说法中正确的是( )
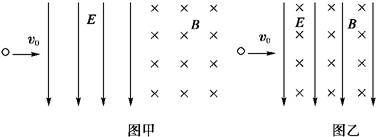
(2008?崇文区一模)某电场的部分电场线如图所示,A、B是一带电粒子仅在电场力作用下运动轨迹(图中虚线)上的两点,下列说法中正确的是( ) (2008?崇文区一模)如图所示,长度为L=0.2m、电阻r=0.3Ω、质量m=0.1kg的金属棒CD,垂直跨搁在位于水平面上的两条平行光滑的金属导轨上,导轨间距离也为L,棒与导轨间接触良好,导轨电阻不计.导轨左端接有R=0.5Ω的电阻,垂直导轨平面的匀强磁场向下穿过导轨平面,磁感强度B=4T.现以水平向右的恒定外力F使金属棒右移,当金属棒以v=2m/s的速度在导轨平面上匀速滑动时,求:
(2008?崇文区一模)如图所示,长度为L=0.2m、电阻r=0.3Ω、质量m=0.1kg的金属棒CD,垂直跨搁在位于水平面上的两条平行光滑的金属导轨上,导轨间距离也为L,棒与导轨间接触良好,导轨电阻不计.导轨左端接有R=0.5Ω的电阻,垂直导轨平面的匀强磁场向下穿过导轨平面,磁感强度B=4T.现以水平向右的恒定外力F使金属棒右移,当金属棒以v=2m/s的速度在导轨平面上匀速滑动时,求: